Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.5 - Ex. 18
Explique porque a função é descontínua no número dado . Desenho o gráfico da função.
Passo 1
Fala aí. Tudo certinho como você?
Bom, esse exercício da pra gente a função
E pede pra gente usar a definição de continuidade e as propriedades dos limites para mostrar que essa função é contínua para .
Então o que precisaremos aqui é saber o que torna uma função contínua em um ponto específico e verificar se isso acontece nessa função que temos aí.
E para que a função seja contínua no ponto a regra é essa aqui:
Uma função é contínua em um número se
Ou seja, aqui temos três condições.
precisar estar definida em (isto é, está no domínio de );
existe;
(o valor do limite é igual ao valor da função no ponto ).
Se isso estiver acontecendo para a função no ponto dado no enunciado, então ela será contínua. Beleza?
Então, bora ver tudo isso acontecendo!
Passo 2
Nesse exercício iremos analisar a função:
No ponto:
Então, vamos primeiro ver se a função está definida nesse ponto e qual o seu valor.
Perceba que ela é uma função dada por partes, e na segunda linha temos exatamente seu valor para . Assim:
Então ela está definida e seu valor é igual a .
Show, agora vamos analisar o limite.
Passo 3
Para calcular o limite precisaremos dos limites laterais, já que o denominador irá se aproximar do zero quando se aproximar de . O que vai fazer o limite ir para o infinit. Mas não sabemos exatamente o seu sinal.
Então, pela esquerda teremos:
Já que o numerador é positivo e o denominador tende a zero por valores negativos.
E, pela direita teremos:
Já que o numerador é positivo e o denominador tende a zero por valores positivos.
Como os limites laterais são diferentes, podemos afirmar que não existe.
Eita!!!
Passo 4
Agora devemos confirmar a condição de continuidade da função no pondo , que diz que:
Mas, como vimos no passo 3.
Então podemos concluir que é descontínua no ponto -2.
Passo 5
Podemos verificar o que foi posto através da análise do gráfico da função a seguir:
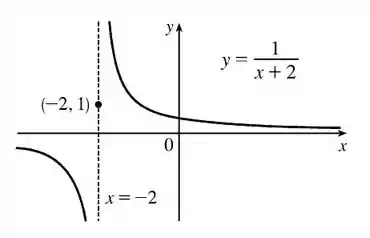
Perceba que realmente a função diverge para menos infinito quando se aproxima de -2 pela esquerda, e pra mais infinito quando se aproxima de pela direita. Mostrando a descontinuidade da função nesse ponto.
Resposta
é descontínua em