Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 2.7 - Ex. 3
Considere a inclinação da curva em cada um dos cinco pontos dados. Classifique-os em ordem decrescente e explique seu raciocínio.
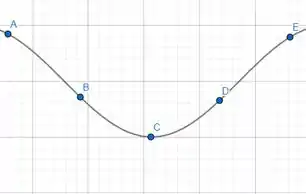
Gráfico com aproximação, mas que mantém as propriedades das tangentes.
Passo 1
Opa, bora lá! Temos a curva:
A gente precisa classificar em ordem decrescente as retas tangentes dos pontos acima!
Os pontos em que a tangente tiver coeficiente angular negativo, falaremos que tem uma inclinação “negativa”. E ao contrário também.
Passo 2
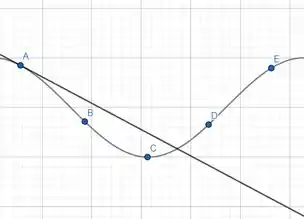
No ponto , temos uma inclinação negativa.
No ponto , temos uma inclinação negativa e uma inclinação maior que em, porém isso torna a inclinação em B mais negativa que em
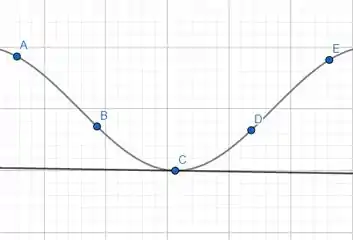
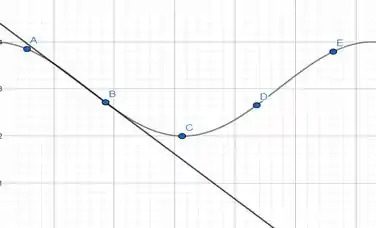
No ponto temos uma inclinação nula, ou seja, não há inclinação.
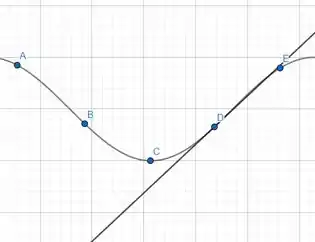
No ponto , temos uma inclinação positiva.
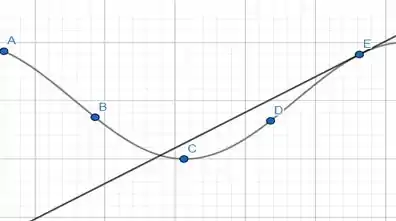
No ponto, temos uma inclinação positiva, porém menor do que em .
Passo 3
Resumindo temos que em e as inclinações são negativas. B é mais inclinado que A, maaass, como são inclinações negativas, então a inclinação de A vai ser maior que a de B.
Em , não há inclinação
E em , as inclinações são positivas e a inclinação em D é maior que em B.
Colocando em ordem decrescente, temos:
Prontinho!