Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 48
O número de franquias de uma certa cadeia popular de cafeterias é mostrada na tabela. (Dados os números de franquias no dia de junho de cada ano.)
- Encontre a taxa média do crescimento:
- Estime a taxa de crescimento instantânea em tomando a média de duas taxas médias da variação. Quais são suas unidades?
- Estime a taxa instantânea de crescimento em medindo a inclinação de uma tangente.
( de a de a de a
Em cada caso, inclua as unidades.
Passo 1
E aí, preparado para mais uma questão sobre taxas de variação? Bora meter ficha!
Para estimarmos as taxas médias pedidas na questão, vamos ter que usar a seguinte equação (onde é o número de franquias da cafeteria, o tempo em anos e a taxa de variação):
Nós pegamos a equação da inclinação de uma reta e adptamos às nossas variáveis, porque a inclinação de uma reta nada mais é do que uma taxa de variação, tranquilo? Esse conceito é importante que só e ta sempre aparecendo em cálculo, então fica atento!
Passo 2
- Para o caso , extraindo os valores da tabela – os pontos e – e jogando na equação:
- Para estimarmos a taxa instantânea de variação no ano , iremos pegar a taxa média entre e e a taxa média entre e .
- Nessa aqui, a gente precisa de uma reta que seja tangente ao ponto . Dá uma olhada em como ficaria o gráfico dos pontos que a gente tem (vermelho) junto com uma reta tangente no ponto que a gente ta estudando (azul):
Para o caso , de forma semelhante, utilizando os pontos e :
Por fim, para o caso , utilizando os pontos e :
Como é dado em franquias e em anos, a unidade de toda e qualquer taxa de variação que encontrarmos aqui nesse exercício vai ser , belê? Bora continuar!
Passo 3
Pegamo esse valores porque uma taxa foi calculada pegando um ponto imediatamente antes de e a outra um ponto imediatamente depois. Sempre pegamos os pontos mais próximos do nosso ponto!
Para fazermos a estimativa, basta tirarmos a média das duas taxas que escolhemos! Vai ficar assim olha:
Passo 4
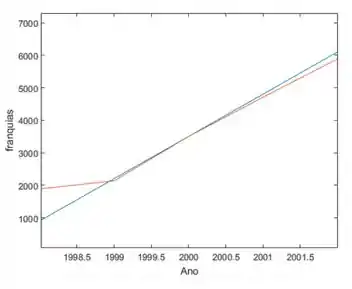
Se a gente pegar essa reta do gráfico, teremos nela o ponto ponto e outro ponto que seria . Jogando isso na nossa fórmula, teremos:
Como o gráfico foi feito no computador, temos mais certeza do valor, mas caso o gráfico fosse feito à mão, teríamos um valor com um certo erro. O importante é lembrar que aqui temos uma estimativa e, se o seu valor não der exatamente esse, não tem problema ;)
Resposta