Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.1 - Ex. 1
Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
Se é o ponto sobre o gráfico de , encontre as inclinações das retas secantes , onde é o ponto sobre o gráfico correspondente a
Estime a inclinação da reta tangente em pela média das inclinações de duas retas secantes.
Use o gráfico da função para estimar a inclinação da reta tangente em . (Essa inclinação representa a taxa segundo a qual a água escoa do tanque após 15 minutos.)
Passo 1
a) Olá, amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
A equação da inclinação () é usado para inserir os vários valores de de acordo com a tabela do passo 1.
Utilizando os dados do ponto , temos que a equação para calcular a inclinação da reta secante é
Temos que o ponto é , ficamos com
Temos que o ponto é , construindo uma tabela para facilitar a visualização, ficamos com
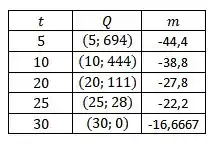
Passo 2
b) A melhor maneira de descobrir a inclinação da reta tangente com base nas linhas secantes () seria a média de todas as cinco pistas.
MAS a pergunta é baseada em apenas duas linhas secantes, então só usaremos e .
Passo 3
c) Fazendo o gráfico
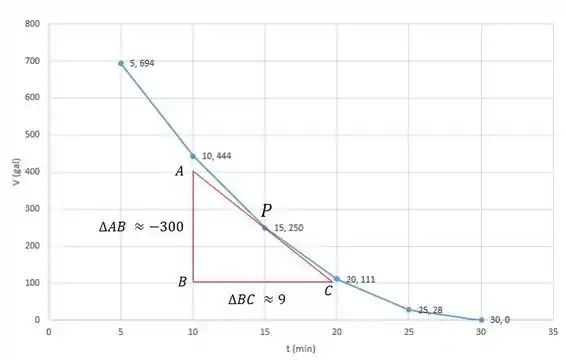
Pelo gráfico, ao tirarmos a tangente de angulo , ficamos com
Resposta
a)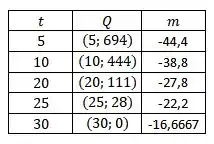 
b)
c)