Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.7 - Ex. 46
Um peru assado é tirado do forno quando sua temperatura atinge e colocado sobre uma mesa na sala, na qual a temperatura é de . O gráfico mostra como decresce a temperatura do peru até aproximar da temperatura da sala. (Na Seção poderemos usar a Lei do Resfriamento de Newton para encontrar uma equação para como uma função do tempo.) Por meio da medida da inclinação da reta tangente, estime a taxa de variação da temperatura após hora.
Passo 1
E aí! tudo certinho? 😊
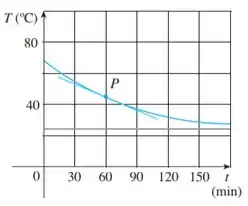
Bom galera, nessa questão temos todo um textinho que não é muito importante pra solução desse problema! O foco aqui é, temos um gráfico da temperatura de um peru de natal que terminou de sair do forno, em função do tempo:
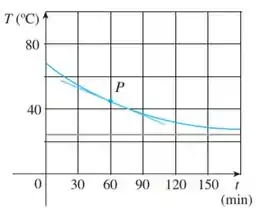
A gente tem que estimar qual a inclinação da reta tangente. Chamaremos essa inclinação de , ok?
A inclinação de qualquer reta pode ser encontrada desse jeito aqui:
Onde são as coordenadas de um ponto qualquer da reta e as coordenadas de outro ponto qualquer.
Essa questão serve para que a gente entenda como é o processo de estimar uma reta tangente sem fazer nenhuma conta. Desenhamos a reta, estimamos dois pontos dessa reta e tiramos uma aproximação da reta tangente, sacou?
Bora lá! 😎
Passo 2
A reta parece ter os pontos e . Se a gente usar esses dados, a nossa inclinação vai ficar desse jeito aqui:
Esses valores são só uma estimativa, então se der diferente o teu resultado, não te preocupa! Tem duas coisas só que podemos ter certeza: será um número negativo (pois temos uma reta decrescente) e a sua unidade será (unidades de dividido por unidades de ). Isso daí tem que aparecer independente do valor numérico, fechou? ;)
O que achou? Responde Aí! 😉
