Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 15.Revisão - Ex. 28

Calcule o valor da integral múltipla.

∫ ∫ ∫ H z 3   x 2 + y 2 + z 2   d V

onde   H é o hemisfério sólido com centro na origem e raio 1 , que está acima do plano x y .

Passo 1

E aí turma, tudo bom com vocês? Vamos lá!

Precisamos calcular a integral a seguir:

∫ ∫ ∫ H z 3   x 2 + y 2 + z 2   d V

onde   H é o hemisfério sólido com centro na origem e raio 1 , que está acima do plano x y .

Como vamos resolver?? Vamos pensar juntos!!!

Vamos precisar reescrever nossa integral de forma que ela possa ser escrita como uma integral iterada, ou seja, uma integral que tem mais de uma variável e possui limites de integração.

Sabemos que d V = d x d y d z , mas isso ainda não nos ajuda.

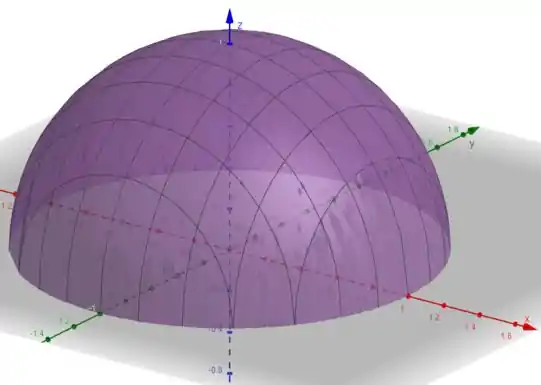
Precisamos entender a região H . Observe que esse hemisfério sólido com centro na origem e raio 1 , que está acima do plano x y , é exatamente meia esfera, porque ele quer somente acima do plano x y .

Tem essa cara:

Logo, nosso objetivo vai ser escrever a integral em coordenadas esféricas. Dessa forma:

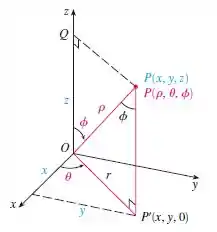
Lembre-se que em coordenadas esféricas o d V fica:

d V =   ρ 2 sin ⁡ ϕ d ρ   d ϕ   d θ

Outro ponto importante, é em relação aos intervalos de integração. O raio ele nos informou que é 1 , e como é meia esfera o ângulo ϕ varia de 0 até π 2 . Logo temos que:

0 ≤ ρ ≤ 1

0 ≤ ϕ ≤ π 2

0 ≤ θ ≤ 2 π

Com essas informações é só montar integral e começar a integrar!!! Bora lá!

Passo 2

Vamos começar então! Temos a seguinte integral:

∫ ∫ ∫ H z 3   x 2 + y 2 + z 2   d V

E já sabemos que nossa região é meia esfera. Logo, em coordenadas esféricas temos que:

x = ρ sin ⁡ ϕ cos ⁡ ( θ )

y = ρ sin ⁡ ϕ sen ⁡ ( θ )

z = ρ cos ⁡ ϕ

E os intervalos são:

0 ≤ ρ ≤ 1

0 ≤ ϕ ≤ π 2

0 ≤ θ ≤ 2 π

Agora já conseguimos montar a integral, é só substituir as variáveis correspondentes. Substituindo vamos ter que:

∫ 0 2 π ∫ 0 π / 2 ∫ 0 1 ( ρ cos ⁡ ϕ ) 3   ( ρ sin ⁡ ϕ cos ⁡ ( θ ) ) 2 + ( ρ sin ⁡ ϕ sen ⁡ ( θ ) ) 2 + ( ρ cos ⁡ ϕ ) 2   ρ 2 sin ⁡ ϕ d ρ   d ϕ   d θ

Sabemos da seguinte relação trigonométrica:

s e n 2   x + cos 2 ⁡ x = 1

Logo podemos simplificar nossa integral acima, que vai ficar:

∫ 0 2 π ∫ 0 π / 2 ∫ 0 1 ( ρ cos ⁡ ϕ ) 3   ρ 2   ρ sin ⁡ ϕ d ρ   d ��   d θ

∫ 0 2 π ∫ 0 π / 2 ∫ 0 1 ρ 6 cos 3 ⁡ ϕ   sin ⁡ ϕ d ρ   d ϕ   d θ

Agora, nosso objetivo é começar a integrar.

Passo 3

Vamos começar a integrar em d ρ . Lembre-se que todos os demais termos que não dependem de ρ são considerados constantes, e isso se aplica as demais variáveis.

Integrando em d ρ , temos que:

∫ 0 2 π ∫ 0 π / 2 sin ⁡ ϕ cos 3 ⁡ ϕ ρ 7 7 0 1   d ρ   d ϕ   d θ

Aplicando os limites de integração temos que:

∫ 0 2 π ∫ 0 π / 2 1 7 sin ⁡ ϕ cos 3 ⁡ ϕ   d ϕ   d θ

Agora vamos integrar em d ϕ . Aqui vamos precisar fazer uma substituição do tipo:

u = cos ⁡ ( ϕ )

d u d ϕ = - sin ⁡ ϕ

- d u = sin ⁡ ϕ d ϕ

Ficando com:

∫ 0 2 π ∫ 0 π / 2 1 7 ⁡ u 3   ( - d u )   d θ

Integrando em d u e voltando a variável ϕ , vamos ter:

∫ 0 2 π - 1 7   ( cos ⁡ ( ϕ ) ) 4 4     0 π 2 d θ

Aplicando os limites de integração vamos ter:

∫ 0 2 π - 1 7   - 1 4     d θ

Passo 4

Por fim, nos restou uma integral simples em d θ .

∫ 0 2 π 1 2 8     d θ

Integrando, vamos ter:

1 2 8 θ 0 2 π

Aplicando os limites de integração, vamos ter como resposta:

1 28 ( 2 π ) = π 14

Resposta

π 14

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

int_0^(2 pi) int_0^((pi)/(4)) int_0^(2 pi) ( rho cos (varphi) rho^2 s e n (varphi) d rho d varphi d theta
int_0^((3)/(2) pi) int_0^(pi) int_0^1 5 rho^3 s e n^3 (varphi) d rho d varphi d theta
int_0^(pi) int_0^(pi) int_0^(2 s e n ( varphi )) rho^2 s e n (varphi) d rho d varphi d theta
Calcule as integrais em coordenadas esféricas:int_0^(2 pi) int_0^((pi)/(4)) int_0^(sec (varphi)) (rho cos (varphi)) rho^2 s e n (varphi) d varphi d varphi d theta
Nos Exercícios 33-38, (a) encontre os limites em coordenadas esféricas para a integral que calcula o volume do sólido dado e em seguida (b) calcule a integral.O sólido delimitado abaixo pelo hemisféri