Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 10.6 - Ex. 20

Considere o problema

α ² u x x = u t ,   0   <   x     < L ,   t > 0 ;

u ( 0 , t ) = 0 ,   u x ( L , t ) + γ u ( L , t ) = 0 ,   t > 0 ;

u ( x , 0 ) = f ( x ) ,   0   ≤   x   ≤   L  

  1. Seja u(x, t) = X(x)T(t) e mostre que

  2. X ' ' + λ X = 0 ,   X ( 0 ) = 0 ,   X ' ( L ) + γ X ( L ) = 0 .

    T ' + λ α ² T = 0 ,

    em que λ é a constante de separação.

  3. Suponha que λ é real e mostre que o problema (ii) não tem soluções não triviais se λ ≤ 0.
  4. Se λ > 0, seja λ = μ2 com μ > 0. Mostre que o problema (ii) só tem soluções não triviais seμ for solução da equação
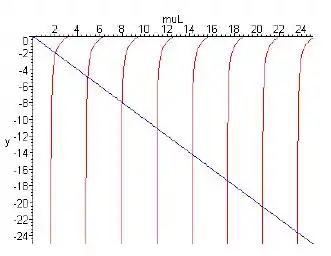
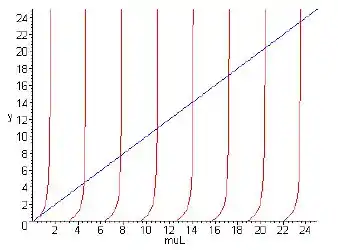
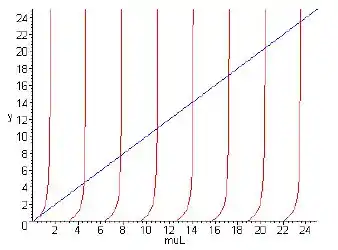
  5. Reescreva a Eq. (iii) como tan(μL) = −μ/γ. Depois, desenhando os gráficos de y = tan(μL) ede y = −μL/γL para μ > 0 no mesmo conjunto de eixos, mostre que a Eq. (iii) é satisfeita por uma infinidade de valores positivos de μ; denote esses valores por μ1, μ2, . . . , μn, . . . ,ordenados em ordem crescente.
  6. Determine o conjunto de soluções fundamentais un(x, t) correspondente aos valores μn encontrados no item (d).

Passo 1

Na letra a:

Temos a seguinte EDP:

α ² X ' ' T = T ' .

Dividindo ambos os lados, obtemos as seguinte EDOs:

X ' ' X = T ' α ² T

X ' ' + λ X = 0 e T ' + λ α ² T = 0 .

Usando as condições de contorno, vamos chegar nessa equação aqui ó:

Para todo t > 0 :

X ( 0 ) = 0 e X ' ( L ) + γ X ( L ) = 0 .

Passo 2

Na letra b:

A solução geral da EDO é:

X ( x ) = c 1 c o s h ( μ x ) + c 2 s e n h ( μ x )

A primeira condição de contorno é c 1 = 0 e a segunda é:

c 2 μ c o s h ( μ L ) + γ c 2 s e n h ( μ L ) = 0 .

Após manipulações matemáticas, chegamos em:

A + γ A L = 0 .

Passo 3

Na letra c:

λ = μ ² ,   c o m   μ > 0 .

Então, a solução geral é:

X ( x ) = c 1 c o s ( μ x ) + c 2 s e n ( μ x ) .

E, utilizando as condições de contorno, chegamos em:

μ c o s ( μ L ) + γ s e n ( μ L ) = 0 .

Passo 4

Na letra d:

A equação pode ser escrita como:

t a n ( μ L ) = - μ γ .

Assumindo γ L = 1 :

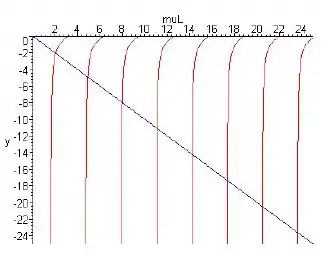
Para γ L =   - 1 :

Passo 5

Na letra e:

A solução geral é:

u ( x , t ) = ∑ n = 1 ∞ c n e - α ² μ n 2 t s e n ( μ n x ) .

Resposta

  1. X ( 0 ) = 0 e X ' ( L ) + γ X ( L ) = 0 .
  2. A + γ A L = 0 .
  3. μ c o s ( μ L ) + γ s e n ( μ L ) = 0 .

  5. u ( x , t ) = ∑ n = 1 ∞ c n e - α ² μ n 2 t s e n ( μ n x ) .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 1 a 8, encontre a solução estado estacionário da equação do calor α 2 u x x = u t que satisfaz o conjunto dado de condições de contorno. u x ( 0 , t ) - u ( 0 , t ) = 0 , u
Suponha que as extremidades de uma barra de cobre com 100 cm de comprimento são mantidas a 0°C. Suponha que o centro da barra é aquecido a 100°C por uma fonte externa de calor; que essa situação se ma
Considere uma barra com 40 cm de comprimento cuja temperatura inicial é dada por u ( x , 0 ) = x ( 60 - x ) / 30 . Suponha que α 2 = 1 / 4 c m 2 / s e que ambas as extremidades da barra estão isoladas
Considere uma barra de alumínio, com 20 cm de comprimento, inicialmente a uma temperatura uniforme de 25°C. Suponha que, no instante t = 0, a extremidade x = 0 é esfriada a 0°C, enquanto a extremidade
Escreva u(x, t) = υ(x) + (x, t), em que υ e são as partes estacionária e transiente,respectivamente, da solução. Enuncie os problemas de valores de contorno que υ(x) e w(x, t)satisfazem, respectivamen