Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.6 - Ex. 4
Considere o problema de valor inicial
(a) Encontre a solução .
(b) A análise de estabilidade no texto sugere que, para esse problema, o método de Euler só é estável para . Confirme se isto é verdade, aplicando o método de Euler a esse problema para com tamanhos de passos próximos de
(c) Aplique o método de Runge-Kutta a esse problema para com diversos tamanhos de passos. O que você pode concluir sobre a estabilidade desse método?
(d) Aplique o método de Euler inverso a esse problema para com diversos tamanhos de passos. Qual o tamanho de passo necessário para que o erro em seja menor do que ?
Passo 1
(a) Precisamos resolver um problema com a condição inicial Primeiro, resolva a equação homogênea correspondente , teremos que a solução é:
Agora encontre a solução específica. É da forma , uma vez que deve ser uma solução do problema inicial, substituímos pelo problema para encontrar e
Se:
A solução do ODE inicial é dada como , portanto, a solução geral é . Mas temos uma condição inicial e podemos determinar :
A solução será:
Passo 2
Para a resolução do passo b usaremos as seguintes fórmulas:
(b) O método Euler afirma que e em que e a condição inicial . O primeiro passo pode ser dado por:
Nós calculamos os passoas até Os valores obtidos estão na tabela a seguir.
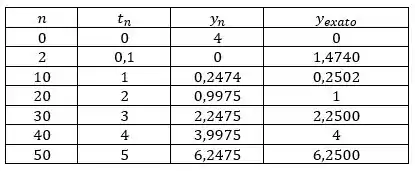
Passo 3
(c) Para este problema, usaremos:
Podemos ter então :
Repetimos os passos até encontrar :
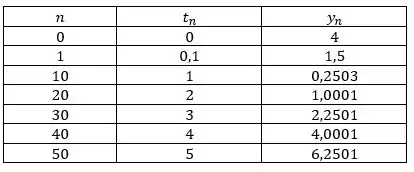
Resposta
- 6,2500
- 6,2501, estável com .