Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.8 - Ex. 24

Considere o problema de maximizar a função f x ,   y = 2 x + 3 y sujeita à restrição x + y = 5 .

(a) Tente utilizar multiplicadores de Lagrange para resolver o problema.

(b) f 25 ,   0 dá um valor maior que o obtido na parte (a) ?

(c) Resolva o problema traçando a equação da restrição e diversas curvas de nível de f .

(d) Explique por que o método dos multiplicadores de Lagrange falha em resolver o problema.

(e) Qual é o significado de f 9 ,   4 ?

Passo 1

Oie, vamos para mais uma resolução. Aqui a gente precisa responder diversas perguntas sobre a maximização da função:

f x ,   y = 2 x + 3 y

Com a restrição:

x + y = 5

Para usar os multiplicadores de Lagrange, a gente utiliza a igualdade:

∇ f = λ ∇ g

Em que ∇ f é o gradiente e é dado por:

∇ f = f x , f y

Para derivar parcialmente devemos derivar em relação a uma variável e considerar todas as outras com constantes.

Com isso em mãos, a gente encontra os valores de x e y resolvendo os sistema com a equação da restrição. Iremos então encontrar um ponto critico que deve ser testado na função f .

Passo 2

  1. Para usar multiplicadores de Lagrange, devemos ter:

∇ f = λ ∇ g

Lembrando que:

f x ,   y = 2 x + 3 y

g x ,   y = x + y

Então vamos derivar parcialmente essas funções:

f x = 2

E

f y = 3

Agora para g :

g x = 1 2 x

E

g y = 1 2 y

Sendo assim, nosso multiplicador é:

2 ,   3 = λ 1 2 x , 1 2 y

Então ficamos com três equações:

2 = λ 2 x                     3 = λ 2 y                     x + y = 5

Passo 3

Isolando x e y nas duas primeiras equações pra jogar na terceira, temos:

x = λ 4

y = λ 6

Jogando na equação:

x + y = 5

λ 4 + λ 6 = 5

λ = 12

Agora que descobrimos o valor de λ , podemos calcular o valor para x e y .

x = 12 4 2 = 9                     y = 12 6 2 = 4

Então, segundo esse método, o máximo seria:

f 9 ,   4 = 2 ⋅ 9 + 3 ⋅ 4

f 9,4 = 30

Passo 4

b) Vamos calcular f 25 ,   0 :

f 25 ,   0 = 2 ⋅ 25 + 3 ⋅ 0

f 25,0 = 50 > 30

Realmente, é um valor maior do que o obtido no item (a) .

Passo 5

  1. Agora vamos traçar a equação da restrição e diversas curvas de nível de f , para traçarmos essas curvas de nível iremos utilizar o GeoGebra, assim como também iremos plotar a equação da restrição.

    2. Veja que para se encontrar a equação da curva de nível de uma função f x , y deveremos igualar a função a uma constante k e plotar o seu gráfico para diferentes valores de k .

    Abaixo temos nosso gráfico:

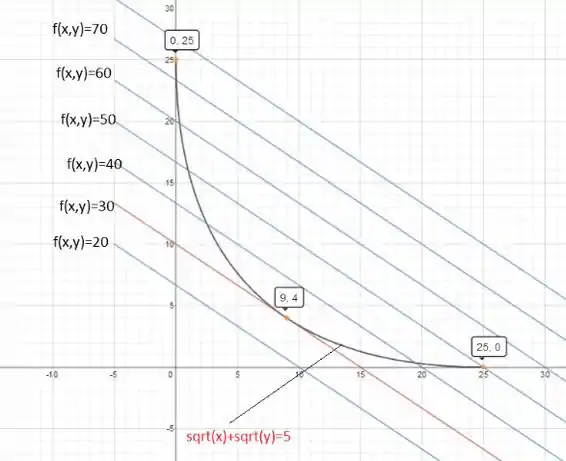
    Então vemos aqui que o máximo da função é:

    f 0 ,   25 = 2 ⋅ 0 + 3 ⋅ 25

    f 0,25 = 75

    Passo 6

  2. O problema de usar multiplicadores de Lagrange aqui é que ∇ g não existe se x = 0 ou y = 0 , por causa do denominador das frações, olha só:

    3. ∇ g = 1 2 x , 1 2 y

    Também o método dos multiplicadores de lagrange identifica pontos onde as curvas de nível de  f  compartilham uma linha tangente comum com a curva de restrição  g .

    Isso normalmente não ocorre em um ponto de extremidade, embora um máximo ou mínimo absoluto possa ocorrer lá

    Passo 7

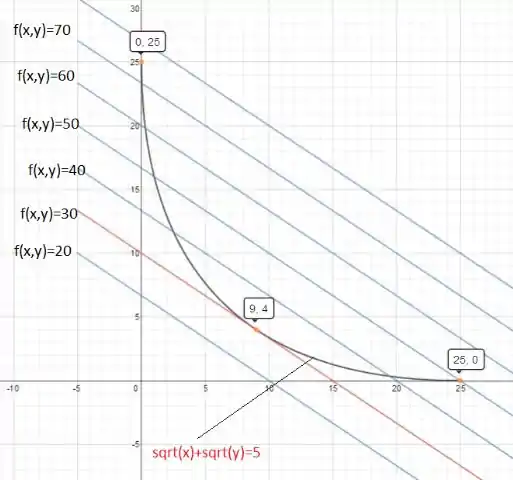
  3. Já que f 9 ,   4 < f 25 ,   0 < f 0 ,   25 , ele deve ser um ponto de mínimo. O gráfico a seguir comprova isso:

Resposta

(a) f 9 ,   4 = 30

(b) Sim

(c) f 0 ,   25 = 75

(d) ∇ g não existe para x = 0 ou y = 0

(e) Ponto de mínimo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use multiplicadores de Lagrange para demonstrar que o triângulo com área máxima, e que tem um perímetro constante p , é equilátero. Dica: Utilize a fórmula de Heron para a área: A = s s - x s - y s -
Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s). f x , y , z , t = x + y + z + t x 2 + y 2 + z 2 + t 2 = 1
16. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s). f x , y , z = 3 x - y - 3 z ; x + y - z = 0 ; x 2 + 2 z 2 = 1