Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 8.5 - Ex. 8

8- Considere o problema de valor inicial

x ' ' + t 2 x ' + 3 x = t ,         x 0 = 1 ,         x ' 0 = 2

Transforme esse problema em um sistema de duas equações de primeira ordem e determine

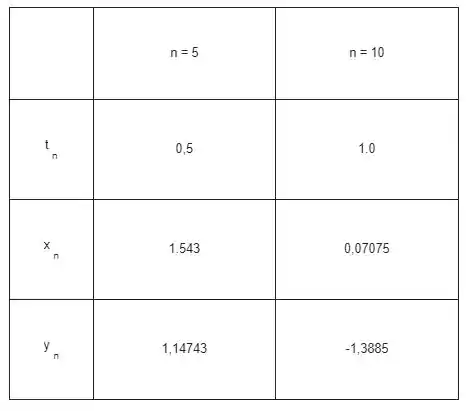
valores aproximados da solução em t   =   0,5 e t   =   1,0 , usando o método de Runge-Kutta com h = 0,1 .

Passo 1

Foi fornecido que temos:

f t , x , y = x ( 1 - 0,5 x - 0,5 y )

g t , x , y = y ( - 0,25 + 0,5 x )

O método Runge-Kutta inclui os seguintes cálculos:

k n 1 = y n , t n - 3 x n - t n 2 y n T

k n 2 = y n + h 2 K n 1 2 , g t n + h 2 , x n + h 2 k n 1 1 , y n + h 2 k n 1 2 T

k n 3 = y n + h 2 K n 2 2 , g t n + h 2 , x n + h 2 k n 2 1 , y n + h 2 k n 2 2 T

k n 4 = f y n + h k n 3 2 , g t n + h ,     x n + h k n 3 1 ,     y n + h k n 3 2 T

Com h = 0 , 1 , os valores obtidos são os seguintes:

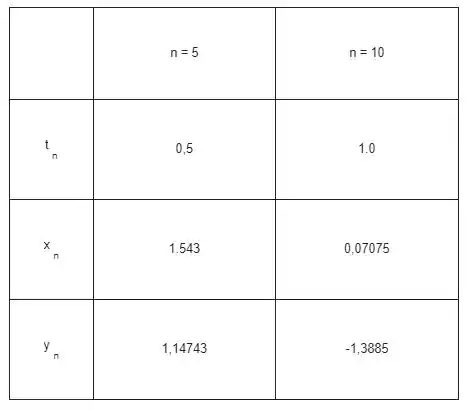
Resposta

a)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

37. Encontre γ, de modo que a solução do problema de valor inicial x 2 y ″ –2 y=0 y 1 =1 y ' ( 1 )= γ permaneça limitada quando x → 0
Em cada um dos problemas de 13 a 16, encontre a solução do problema de valor inicial dado. Faça o gráfico da solução e descreva como ela se comporta quando x → 0 15. x 2 y ″ -3 x y ' +4 y=0 , y ( – 1
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.20. x 2 ( 1–x 2 ) y ″+( 2 / x ) y '+4 y=0
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.23. ( x+3 ) y ″-2 x y '+( 1–x 2 ) y=0
Em cada um dos problemas de 17 a 34, encontre todos os pontos singulares da equação dada e determine se cada um deles é regular ou irregular.19. x 2 ( 1–x ) y ″+( x–2 ) y '–3 x y=0