Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.3 - Ex. 55

Considere a região delimitada pelos gráficos de y = sin - 1 ⁡ x , y = 0 e x = 1 / 2

  1. Determine a área da região
  2. Determine a centroide da região

Passo 1

Primeiro, vamos observar o gráfico da função y = sin - 1 ⁡ x .

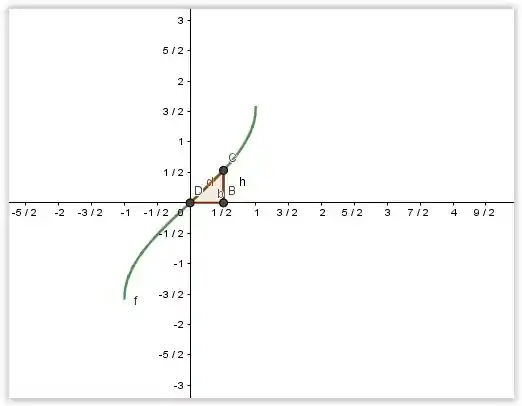
Queremos a área da região quando y = 0 e x = 1 / 2 , que corresponde a região em vermelho, no gráfico, para isso vamos utilizar precisar integrar a função y = sin - 1 ⁡ x , e utilizar os limites de integração para os pontos dados. Então vamos lá:

A =   ∫ 0 1 / 2 sin - 1 ⁡ x   d x

Vamos precisar fazer uma substituição:

u =   sin - 1 ⁡ x         d u =   1 1 - x 2

d v = d x           v = x

Assim,

A = [ x .   sin - 1 ⁡ x ] 0 1 2 -   ∫ 0 1 / 2 x 1 - x 2   d x

=   1 2 sin - 1 ⁡ 1 2 - 0   +   1 - x 2   1 ¦ 0  

=   π + 6 3 - 12 12

Passo 2

Queremos o centroide, ou seja, o centro de massa. Façamos:

Então devemos encontrar:

x - =   ∫ x d A A

y - = ∫ y d A A

z - = ∫ z d A A

Então, façamos:

x - =   ∫ 1 π + 6 3 - 12 12 ∫ 0 1 2 x sin ⁡ x   d x

= 12 π + 6 3 - 12   1 2 x 2 sin - 1 ⁡ x   1 2 0 - 1 2 ∫ 0 1 2 x 2 1 - x 2   d x  

Agora, vamos fazer a seguinte substituição trigonométrica:

x = sin ⁡ θ   d θ

d x = cos ⁡ θ   d θ

1 - x 2 = cos ⁡ θ

Logo,

x = 0 = sin ⁡ θ → θ = 0

x = 1 2 = sin ⁡ θ → θ = π 6

= 12 π + 6 3 - 12   (   1 2 1 2 2 sin - 1 ⁡ 1 2 - 0 - 1 2 ∫ 0 π / 6 sin 2 ⁡ θ cos ⁡ θ cos ⁡ θ d θ )  

= 12 π + 6 3 - 12   π 48 - 1 2 ∫ 0 π 6 sin 2 ⁡ θ   d θ

= 12 π + 6 3 - 12 π 48 - 1 2 ∫ 0 π 6 1 - cos ⁡ 2 θ 2 ⁡   d θ  

= 12 π + 6 3 - 12 π 48   - 1 4 ∫ 0 π 6 d θ + 1 4 ∫ 0 π 6 cos ⁡ 2 θ d θ  

= 12 π + 6 3 - 12   π 48   + - θ 4 + 1 8 sin ⁡ 2 θ π 6 0 =   3 3 - π 4 ( π + 6 3 - 12 )      

Passo 3

Agora, vamos encontrar y -

y - =   1 π + 6 3 - 12 12 ∫ 0 1 2 1 2 ( sin - 1 ⁡ x ) 2 d x

Fazemos a seguinte substituição:

u = ( sin - 1 ⁡ x ) 2

d u = 2 sin - 1 ⁡ x 1 - x   d x

d v = d x

v = x

Assim,

=   6 π + 6 3 - 12   x ( sin - 1 ⁡ x ) 2 d x 1 / 2   0 - ∫ 0 1 2 2 x sin - 1 ⁡ x 1 - x 2   d x

Fazemos a seguinte substituição:

u = ( sin - 1 ⁡ x )

d u = 1 1 - x   d x

d v = 2 x 1 - x 2

v = - 2 1 - x 2

= 6 π + 6 3 - 12 1 2   sin ⁡ 1 2 2 - 0 + 2 1 - x 2 sin - 1 ⁡ x   1 2 0 - ∫ 0 1 2 2 1 - x 2 1 - x 2 d x  

= 6 π + 6 3 - 12   π 2 72 + 2 1 - 1 2 2 sin - 1 ⁡ 1 2 - 0 - 2 x 1 2 ¦ 0  

= 6 π + 6 3 - 12 π 2 72 +   π 3 6 - 1 = π 2 + 12 3 - 72 12 ( π + 6 3 - 12 )

Resposta

  1.   π + 6 3 - 12 12
  2. 6 π + 6 3 - 12 π 2 72 +   π 3 6 - 1 = π 2 + 12 3 - 72 12 ( π + 6 3 - 12 )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

4. Calculej)int (1)/(x^2 + 2 x + 5) d x
4. Calculef)int (x - 1)/(sqrt(2 x + 1)) d x
Calculeint sqrt(1 - e^x) d x
Calculeint x a r c s e n x d x
Calculeint sqrt(1 + sqrt(x)) d x