Considere os segmentos de curva de até e o segmento de curva de até
(a) Faça o gráfico dos dois segmentos de curva e utilize-os para explicar por que os comprimentos desses dois segmentos deveriam ser iguais.
(b) Monte integrais que deem os comprimentos de arco dos dois segmentos de curva, com integração em relação a Demonstre com uma substituição que essas duas integrais são iguais.
(c) Monte integrais que deem os comprimentos de arco dos dois segmentos de curva, com integração em relação a .
(d) Aproxime o comprimento de arco de cada segmento de curva usando a Fórmula (2) com subintervalos iguais.
(e) Qual das duas aproximações em (d) é mais precisa? Explique.
(f) Use a aproximação pelo ponto médio com n = 10 subintervalos para aproximar cada integral de comprimento de arco em (d).
(g) Use uma calculadora com integração numérica para aproximar cada integral de comprimento de arco em (b) até quatro casas decimais.
Passo 1
E aí, tudo joia?
Essa aqui é grandinha hein? Mas vamos por partes. Primeiro o gráfico:
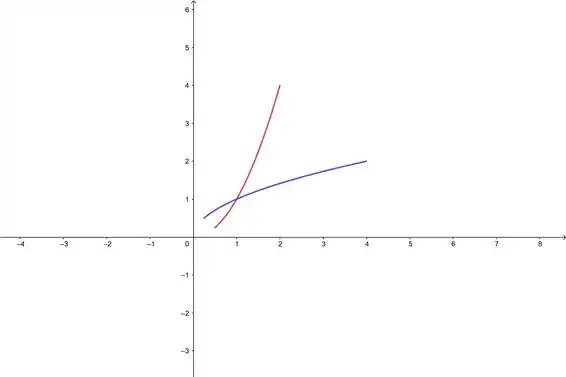
Olha só, aqui a gente já consegue ver que são iguais né? E olha só:
Jogando os extremos de nela, a gente encontra os limites de integração da outra:
Então, nada mais esperável que tenhamos comprimentos iguais aqui né? A gente vai ver isso com mais detalhes...
Passo 2
b) Montamos as integrais agora que calculam os comprimentos:
Primeiro para o caso:
Aí teremos a derivada:
A integral do comprimento então fica:
Usando a outra função:
E aí aplicando na fórmula:
Passo 3
Vamos lá na primeira e fazer a substituição:
E aí os limites de integração viram:
Aí a gente vai ter:
Veja que é a mesma integral de , mudando apenas a variável. Assim, provamos que as expressões para o comprimento são iguais.
Passo 4
c) Vamos passar essas funções para .
E aí aqui os limites de integração vão ser:
E aí os limites de integração ficam:
Montamos as integrais de comprimento então assim:
E a outra:
Nada de novo até aqui né?!
Passo 5
Vamos fazer a substituição:
Como a gente vai substituir isso na segunda integral, teremos os limites de integração elevados ao quadrado, sendo:
Vai ficar:
Que é exatamente igual à outra integral, mudando apenas a variável😉
Passo 6
d) Aqui a gente vai usar essa fórmula aqui:
Vamos aplicar primeiro na função
Vai ficar:
E daí os valores do somatório vão variando nessa intensidade. Começando em , teremos:
(aplicando em todos os 10 termos e somando)
Isso vai nos dar:
Passo 7
A gente vai fazer a mesma coisa na função de até , também com 10 subintervalos.
Aqui o nosso vai ser:
Ou seja, começando em , vamos variando até chegar no .
O nosso somatório vai ficar:
Aí a gente vai expandir e aplicar isso nos 10 termos:
(escrevi só o primeiro e o último aqui pra você entender o esquema)
Resolvendo e somando esses 10 termos, a gente encontra aproximadamente:
Passo 8
e) A primeira aproximação é mais precisa, porque o segundo somatório contém muitos termos com raiz quadrada, e nas aproximações acabam perdendo umas casas decimais.
Passo 9
f) Agora vamos usar a fórmula:
Sabendo que .
Na primeira função, com , teremos:
Aí
E assim por diante...
Jogando isso no somatório e expandindo, a gente vai ter:
Passo 10
Na segunda função agora:
Aqui a gente tem , sendo .
Expandindo o somatório e resolvendo, a gente vai achar:
(essa deu um pouco de discrepância...)
Passo 11
g) Vamos calcular as integrais agora:
Vou calcular no Desmos:
Ufaaaa!!! Acabamos por aqui😉
Resposta
- Gráficos.
- A primeira.