Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 30
30- O sistema de dois tanques do Problema na Seção nos leva ao problema de valor inicial
Em que e são os desvios dos níveis de sal e dos seus respectivos pontos de equilíbrio
Encontre a solução do problema de valor inicial dado
Faça os gráficos de e de em função de no mesmo conjunto de eixos
Encontre o menor instante tal que e para todo
Passo 1
Esse problema é a soma de praticamente tudo que fizemos nas questões anteriores, isso quer dizer que ele dá mais trabalho hahahah
Encontrando os autovalores dessa matriz nós temos:
Então:
Passo 2
O auto valor nos dá um autovetor igual a e que será:
O que nos dá:
Fazendo a multiplicação vetorial nós temos algo como:
O autovetor associado ao autovalor será:
Então a solução será:
Passo 3
Agora para nós temos o autovetor :
Isso nos dá uma relação igual a:
O que nos dá um autovetor igual a:
Logo uma solução igual a:
Então a solução geral estará na forma de:
Passo 4
Agora vamos aplicar o valor inicial para encontrar e e fazendo isso nós teremos:
Ou seja em é e em é logo:
Então:
Multiplicando a primeira equação por nós vamos ter:
Somando:
Então será:
Então a solução geral será igual a:
Passo 5
Pela solução geral teremos que o valor de e de são:
Portanto:
Plotando o gráfico das duas equações na mesma imagem nós teremos:
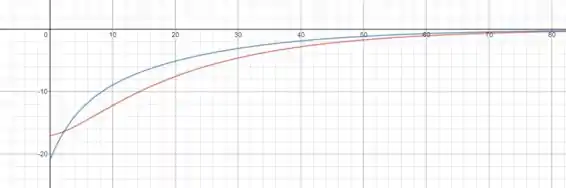
Onde é a curva vermelha e a azul.
Passo 6
Queremos saber na letra o tempo onde as duas funções terão valor de módulo menor que e como as duas funções são crescentes (de forma monótona) e em e tendem a zero, logo para (que é a curva que sempre nos dará valores de maior intensidade) nós teremos:
No gráfico vemos que esse tempo se dará em , nesse valor já tem um módulo menor que há um tempo já.