Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 7.5 - Ex. 24
Em cada um dos problemas de a , são dados os autovalores e autovetores de uma matriz . Considere o sistema correspondente .
Esboce um retrato de fase do sistema
Esboce a trajetória que contém o ponto inicial
Para a trajetória no item . Esboce os gráficos de e de em função de no mesmo conjunto de eixos.
Passo 1
A solução geral desse sistema será:
E essa matriz será dita como:
Portanto iremos encontrar os valores dessa matriz fazendo:
Na primeira equação teremos:
E da segunda equação:
Da primeira e terceira equação nós encontramos:
E da segunda e da quarta nós teremos:
O que nos dá o seguinte sistema:
Considerando nós teremos:
A representação vetorial desse sistema será:
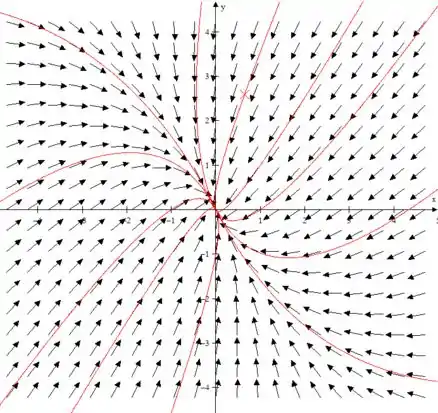
Passo 2
Para a letra basta colocar e na equação diferencial onde a primeira linha se trata de e a segunda de , (na verdade é e mas no winplot finge que é e para dar certo), então:
Ou seja nesse caso colocamos e . é a reta horizontal. E como a linha é decrescente em então só teremos a parte a esquerda do ponto.
Passo 3
Seguindo o mesmo raciocínio é como se tivéssemos:
Então:
Então para e e , nós teremos:
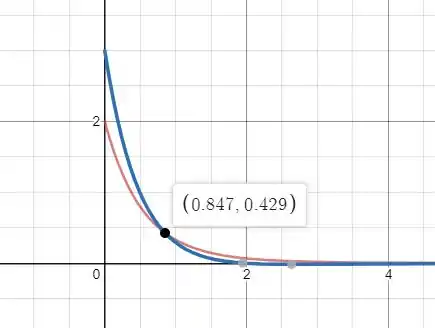
Plotando esse gráfico nós obteremos sendo a curva vermelha e a azul. As curvas de e assim como o retrato de fase representam um sistema estável.