Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 9

Considere a superfície S obtida girando-se o segmento de reta que liga os pontos ( 1,0 , 1 ) e ( 0,0 , 3 ) em torno do eixo z . Calcule

∬ S r o t   F   .   n   d s ,

onde n é o campo de vetores normais exterior a superfície a S e F é um campo vetorial em R 3 definido por

F x , y , z = - y 3 3 + z e x , x 3 3 - c o s y z , x y .

Passo 1

Se liga! Podemos começar esboçando o desenho do sólido gerado pelo giro do segmento de reta.

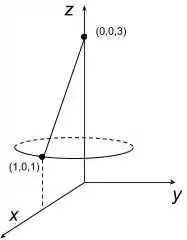
Quando giramos o segmento de reta em torno do eixo z , formamos um cone. Estamos interessados na superfície lateral ( S ) do cone.

Uma sacada para facilitar nossas contas é completar com a base ( D ) para fechar o sólido e poder usar o Teorema de Gauss.

Passo 2

Como agora temos uma superfície fechada, podemos usar o teorema de Gauss.

∬ S ∪ D F →     .   n →   d s = ∭ W d i v F → d V

Separando a primeira integral para as duas regiões, temos

∬ S r o t   F →     .   n →   d s + ∬ D r o t   F →     .   n →   d s = ∭ W d i v r o t   F → d V

Passando a parte correspondente a região D , para o outro lado, temos

∬ S r o t   F →     .   n →   d s = ∭ W d i v r o t   F → d V - ∬ D r o t   F →     .   n →   d s

Passo 3

Usar o Teorema de Gauss facilitou um pouco as coisas, pois pelas identidades o divergente do rotacional é sempre zero.

d i v   r o t   F = 0 .

Portanto

∭ W d i v r o t   F → d V = 0 .

Assim podemos concluir que

∬ S r o t   F →     .   n →   d s = - ∬ D r o t   F →     .   n →   d s .

Passo 4

Agora vamos calcular o r o t   F .

r o t   F =   i j k ∂ ∂ x ∂ ∂ y ∂ ∂ z - y 3 3 + z e x x 3 3 - c o s y z x y = x - y s e n   y z ,   e x - y ,   x 2 + y 2 .

Passo 5

Podemos fazer a parametrização de D .

Como o campo está saindo, podemos dizer que ele é paralelo ao eixo z e orientado para baixo. Portanto

n = 0,0 , - 1 .

Como nosso interesse é um disco de raio 1 no plano x y , temos

ϕ x , y = x , y , 0

Portanto

r o t   F x , y , 0 = x ,   e x - y ,   x 2 + y 2 .

Passo 6

Já que já temos a parametrização, podemos montar a nossa integral e resolve-la

∬ D x ,   e x - y ,   x 2 + y 2 0,0 , - 1   d S = ∬ D - x 2 + y 2   d S

Podemos usar coordenadas polares

x = r   c o s θ

y = r   s e n θ

onde

0 ≤ r ≤ 1

0 ≤ θ ≤ 2 π   .

Agora nossa integral é

∫ 0 2 π ∫ 0 1 - r 3 d r d θ = - ∫ 0 2 π r 4 4 0 1     d θ = - ∫ 0 2 π 1 4     d θ = - 2 π 4 = - π 2

Portanto

∬ D r o t   F →     .   n →   d s = - π 2 .

Passo 7

Como vimos antes

∬ S r o t   F →     .   n →   d s = - ∬ D r o t   F →     .   n →   d s

Sendo assim

∬ S r o t   F →     .   n →   d s = π 2 .

Resposta

∬ S r o t   F →     .   n →   d s = π 2 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = x 2 y , 2 x z , z 2 e S a superfície exterior do paralelepípedo retangular delimitado pelos pla
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = ( 0,0 , 2 z ) e S a superfície do Exercício 13, exceto a face superior.
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S ( 2 d y d z + 3 d z d x - 5 d x d y ) onde S é a superfície do paraboloide z = 9 - x 2 - y 2 acima do plano z = 0 .
Usar o teorema da divergência para calcular a integral da superfície dada. ∬ S f → ⋅ n → d S Sendo f → = ( 2 x , 2 y , 0 ) e S a superfície do Exercício 13, exceto a face superior.
Usar o teorema da divergência para calcular o fluxo do campo vetorial f → , através da superfície do sólido T ,sendo: f → = 2 i ^ + 2 j ^ = 2 k ^ e T a esfera x 2 + y 2 + z 2 ≤ 4