Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.2 - Ex. 6a

Considere a superfície parametrizada por

φ r , θ = r cos ⁡ θ ,   r sin ⁡ θ ,   θ                 0 ≤ r ≤ 1               0 ≤ θ ≤ 4 π

  1. Esboce essa superfície.

Passo 1

Queremos fazer um esboço da superfície φ r , θ = r cos ⁡ θ ,   r sin ⁡ θ ,   θ . Notemos que:

x = r cos ⁡ θ

y = r sin ⁡ θ

Logo,

x 2 + y 2 = r cos ⁡ θ 2 + r sin ⁡ θ 2 x 2 + y 2 = r 2 cos 2 ⁡ θ + sin 2 ⁡ θ

Mas sabemos que cos 2 ⁡ θ + sin 2 ⁡ θ = 1 para todos os valores de θ . Assim,

x 2 + y 2 = r 2

Assim, como 0 ≤ r ≤ 1 , segue que quando θ varia, a superfície vai descrevendo círculos de raio 0 ≤ r ≤ 1 .

Passo 2

Logo, quando θ vai indo de 0 até 4 π , vamos andando ao longo do eixo z , enquanto vamos descrevendo círculos paralelos ao plano x y .

Passo 3

Veja a figura:

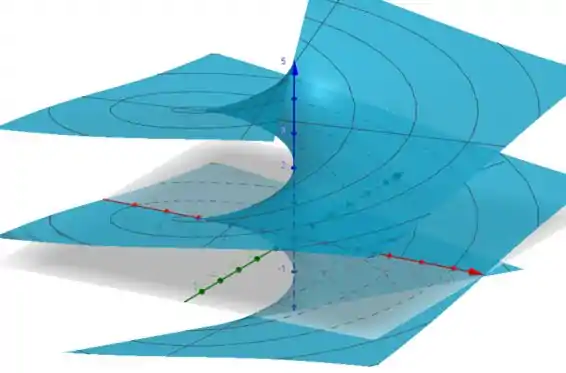
Resposta

Ver figura.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f a transformação de R 2 em R 3 dada por x , y , z = ( u + v , u , v ) . Mostre que f transforma o plano u v no plano x - y - z = 0 .
Seja f (u , v) = ( u , v , 1 - u - v ) , com u = 0 , v = 0 e u + v = 1 . Desenhe a imagem de f .
2. a. Encontre uma parametrização para a superfície obtida girando-se o circulo x - a 2 + z 2 = r 2,0ra , torno do eixo z. Esta superfície é chamada de toroB . Encontre um vetor normal a essa superfíc
1 . Seja S uma superfície parametrizada por φ u , v = v cos ⁡ u ,v s e nu , 1 - v 2 0u2 π v ≥ 0 Identifique esta superfície. Esta superfície é regular ? Trace as curvas na superfice S. Definidas por φ
3. Considere as superfícies S 1 e S 2 parametrizadas por φ 1 u , v = u , v , 0 φ 2 u , v = u 3 , v 3 , 0 u , v ∈ R 2 Respectivamente Mostre que S1 e S2 são o plano XYMostre que S1 é regular e que S3 n