Enunciado
Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.2 - Ex. 3
3. Considere as superfícies e parametrizadas por
Respectivamente
- Mostre que S1 e S2 são o plano XY
- Mostre que S1 é regular e que S3 não o é. Conclua que a regularidade de uma superfície S depende da existência de pelo menos uma parametrização na qual S seja regular
- É possivel encontrar uma parametrização na qual o cone da figura 7.4 seja regular em
Passo 1
- Quando queremos saber com que superfície estamos trabalhando, eu sugiro sempre que voltemos pra coordenadas cartesianas. Estamos usando esse tipo de coordenadas há muitos anos. É mais fácil pra gente enxergar as coisas nelas. Então temos
- Quando estamos trabalhando com quadricadas, usar a definição de “não há bicos” para definir sua regularidade é prático. Agora quando Temos um plano , temos que usar a definição formal
Está percebendo que nem x nem y possuem limitações ? logo isso é um indicativo que estamos trabalhando com algum plano, existir duas variáveis independentes. E por fim temos
Essa é a equação do Plano XY. Simples assim. Quando olhamos para a outra parametrização
Vemos a mesma coisa. X e Y independentes e . Logo também estamos trabalhando com o plano XY
Passo 2
Nossa superfície é regular se o vetor normal é não nulo em Todo o Dominio! Isso implica que as derivadas parciais não podem se anular em ponto algum. Se analisarmos vemos o seguinte
Cujas derivas parciais são
Essas derivadas são constantes, logo nunca se anulam. Com isso nosso vetor normal também não se anula. Como podemos ver abaixo
O que não acontece com , pois
Cujas derivas parciais são
Essas derivadas se anulam quando e , logo nossa normal também vai se anular em alguns pontos. Logo essa parametrização de superfície não é regular.
Passo 2
C. Então, existem duas respostas pra essa pergunta. Uma curta e simples, outra mais formalizada.
A curta – Para ser regular uma superfície não pode ter bicos. E um cone é pontudo, como podemos ver na figura abaixo
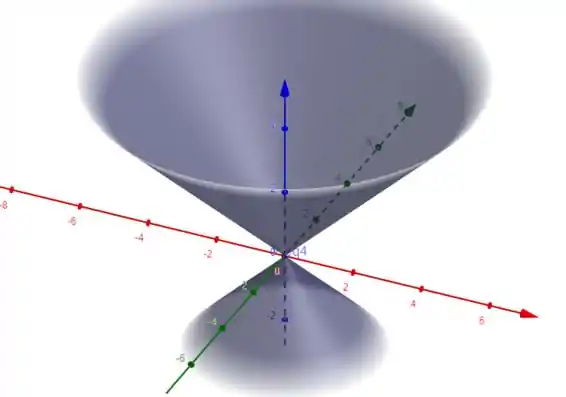
Logo não tem como existir nenhuma parametrização que mudasse esse fato, pois é da própria geometria ele ser assim. As parametrizações apenas tentam escrever em “outras línguas” a mesma figura, mas nunca alterando sua forma. Logo um cone não é regular em
Agora a definição formal – As derivadas parciais desse sistema têm que existir em todo o domínio e não se anular. Se olharmos para a equação da figura 7.4 temos
Ou uma possível parametrização simplinha
Então nossas derivadas parciais são
Essas derivadas nem estão definidas no ponto logo não é possivel que exista regularidade neste ponto.
Terminamos por aqui. Pode comemorar! \o/
Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)