Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.2 - Ex. 1

1 . Seja S uma superfície parametrizada por

φ u , v = v cos ⁡ u ,   v s e n   u , 1 - v 2

0 < u < 2 π

v ≥ 0

  1. Identifique esta superfície. Esta superfície é regular ?
  2. Trace as curvas na superfice S. Definidas por φ u 0 ,   v   e φ u   ,   v 0 onde

    3. i )   u 0 = 0

    i i   )   u 0 = π 2

    i i i )   v 0 = 0

    i v   )   v 0 = 1

  3. Encontre um vetor tangente à curva , definida por φ 0 , v no ponto φ 0,1
  4. Encontre um vetor tangente à curva , definida por φ u , 1 ,   no ponto φ 0,1
  5. Encontre uma equação da reta normal e a equação do plano tangente a S em φ 0,1

Passo 1

  1. Quando temos uma parametrização podemos fazer o seguinte

φ u , v = v cos ⁡ u ,   v s e n   u , 1 - v 2

Pegamos nossa parametrização e olhamos para z. Essa região tem a função z definida como

z =   1 - v 2

Agora basta descobrirmos v. Temos as parametrizações x e y

x = v cos ⁡ u  

  y =   v   s e n   u

Podemos usar a seguinte relação

v 2 cos 2 ⁡ u + v 2 sen 2 ⁡ u = v 2

Logo podemos escrever que

x 2 + y 2 = v 2

Show!!! Então podemos dizer que nossa superfície é

z = 1 - x 2 + y ²

Podemos ver essa superfície abaixo

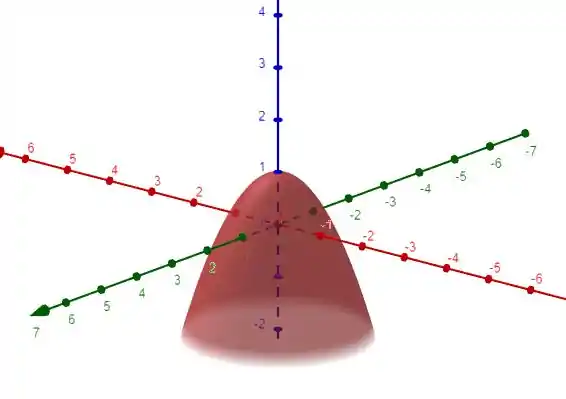
E o enunciado termina perguntando se é regular. Superfícies regulares não tem “bicos” logo essa é uma superfície regular

Passo 2

b. Agora queremos curvas especificas dentro dessa superfície. Pegando

φ u , v = v cos ⁡ u ,   v s e n   u , 1 - v 2

E fazendo

φ u 0 ,   v   e φ u   ,   v 0

  1. u 0 = 0

    2. φ 0 , v = v , 0,1 - v 2

    Ou seja temos a curva z = 1 - x 2 no plano y = 0. Temos então essa curva

  2.   u 0 = π 2

    3. φ π 2 , v = 0 , v , 1 - v 2

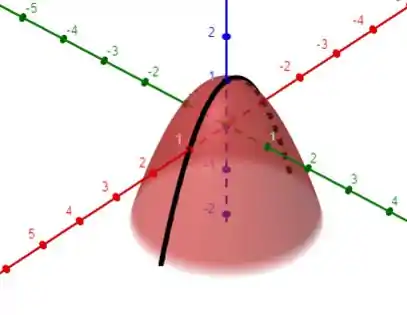
    Ou seja

    z = 1 - y 2

    No plano x = 0. O que gera essa curva

  3.   v 0 = 0

    4. φ u , 0 = 0,0 , 1

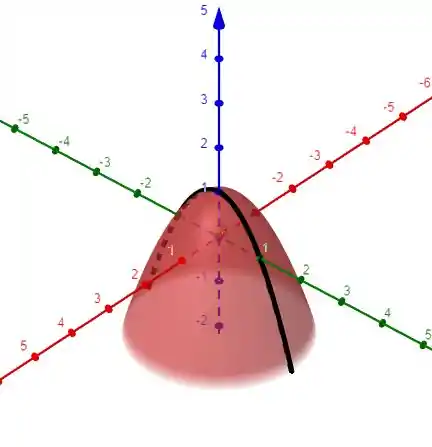
    Que é apenas um ponto.

  4. v 0 = 1

φ u , 1 = cos ⁡ u ,   s e n   u , 0

É um circulo de raio 1 no plano xy , z = 0

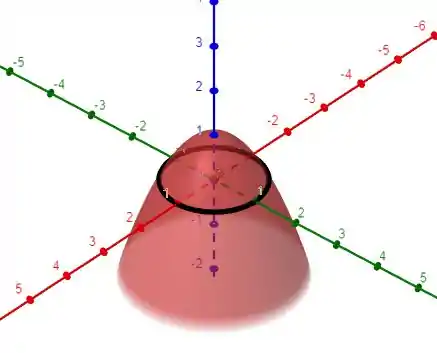
Passo 3

c. Queremos o vetor tangente na curva

φ 0 , v = v , 0,1 - v 2

Então podemos fazer o seguinte. Calcular o vetor derivada parcial dessa curva

∂ φ ∂ v 0 , v = 1,0 , - 2 v

Agora se quisermos a derivada parcial num ponto específico podemos aplicar esse ponto ao nosso cálculo

∂ φ ∂ v 0,1 = 1,0 , - 2

Passo 4

d. Mesmo esquema do item c) sendo que em outra curva

φ u , 1 =   cos ⁡ u ,   s e n   u , 0  

Vamos calcular a derivada parcial

∂ φ ∂ u u , 1 = - sen ⁡ u ,   cos ⁡ u , 0

Agora aplicamos o ponto que queremos a esse vetor

∂ φ ∂ u 0,1 = 0 ,   1,0

Passo 5

Para calcular a reta normal no ponto 0,1 podemos fazer o seguinte

N =   ∂ φ ∂ u 0,1 × ∂ φ ∂ v 0,1

N = i → j → k → 0 1 0 1 0 - 2

N = - 2,0 , - 1

Esse é o vetor da reta normal. Para ser uma reta mesmo Precisamos de um ponto, no nosso caso é o u , v = 0,1 .   Precisamos descobrir o que esse par ordenado faz acontecer em R³

φ 0,1 = 1,0 , 0

Logo Nossa reta pode ser escrita como

N = 1,0 , 0 + - 2,0 , - 1 t    

Passo 6

Agora precisamos achar o plano tangente ao ponto u , v = 0,1 . Podemos usar o vetor da reta Normal para isso

N = - 2,0 , - 1

Logo nossa equação do plano genérico é

a x + b y + c z + d = 0

Onde a,b,c são as coordenadas do nosso vetor normal. Com isso nosso plano tangente é

- 2 x - z + d = 0

Precisamos descobrir d. Para isso vamos usar o ponto

φ 0,1 = 1,0 , 0

- 2   1 + 0 + d = 0

d =   2

Logo o plano é

- 2 x + z + 2 = 0

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

a.

z = 1 - x 2 + y ²

Regular

c.

∂ φ ∂ v 0,1 = 1,0 , - 2

d.

∂ φ ∂ u 0,1 = 0 ,   1,0

e.

N = 1,0 , 0 + - 2,0 , - 1 t    

- 2 x + z + 2 = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Identifique a superfície que tem a equação paramétrica dada. r → u , v = 2 s e nu i → + 3 cos ⁡ u j → + v k → ,0 ≤ v ≤ 2
Encontre uma parametrização para o hiperboloide x 2 + y 2 - z 2 = 1 .
Considere a superfície parametrizada por φ r , θ = r cos ⁡ θ ,r sin ⁡ θ ,θ 0 ≤ r ≤ 10 ≤ θ ≤ 4 π Esboce essa superfície.
Dada a esfera de raio 2 , centrada na origem, encontra a equação do plano tangente a ela no ponto 1,1 ,2 , considerando a esfera como:c) o gráfico de g x , y = 4 - x 2 - y 2 .
Dada a esfera de raio 2 , centrada na origem, encontre a equação do plano tangente a ela no ponto 1,1 , 2 , considerando a esfera como:Uma superfície parametrizada por φ ϕ ,θ = 2 sin ⁡ ϕ cos ⁡ θ ,2 si