Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.2 - Ex. 2

2. a. Encontre uma parametrização para a superfície obtida girando-se o circulo x - a 2 + z 2 = r 2   ,   0 < r < a , torno do eixo z. Esta superfície é chamada de toro

B . Encontre um vetor normal a essa superfície

c. Esta superfície é regular ?

Passo 1

As parametrizações de superfície em geral têm um formato fixo. Por exemplo quando temos um círculo. Em coordenadas cartesianas temos

x 2 + y 2 = r 2

Já em paramétricas teremos algo neste formato

σ t = r cos ⁡ t ,   r sen ⁡ t

Tendeu? A gente não precisa ficar pensando mil jeitos de resolver. já é algo tabelado. Do mesmo forma a equação da tiroide também é. E temos a seguinte parametrização

σ u , v = R + r cos ⁡ v cos ⁡ u , R + r cos ⁡ v sin ⁡ u ,   r sin ⁡ v  

Neste caso a simetria de rotação é em z

Onde r é o raio do círculo quer vai ser revolucionado

R é o raio da tiroide em si, ou seja do centro da tiroide ate o centro do tubo

Passo 2

No nosso caso temos

x - a 2 + z 2 = r 2  

0 < r < a

torno do eixo z. Então nossa parametrização pode ser escrita como

σ u , v = a + r cos ⁡ v cos ⁡ u , a + r cos ⁡ v sin ⁡ u ,   r sin ⁡ v  

Então conseguimos essa superfície

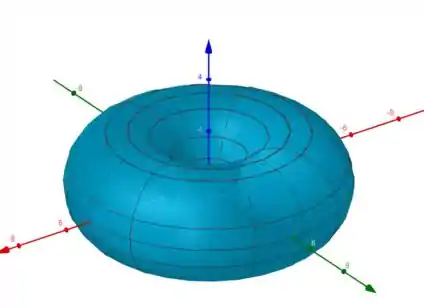
Passo 3

b. O vetor normal pode ser obtido fazendo o produto vetorial das derivadas parciais, então vamos cair dentro

σ u , v = a + r cos ⁡ v cos ⁡ u , a + r cos ⁡ v sin ⁡ u ,   r sin ⁡ v  

∂ σ ∂ u = - a + r cos ⁡ v sin ⁡ u , a + r cos ⁡ v cos ⁡ u , 0  

∂ σ ∂ v = - r sin ⁡ v cos ⁡ u , - r sin ⁡ v sin ⁡ u ,   r cos ⁡ v  

Com isso nosso vetor normal pode ser descrito como

N = ∂ σ ∂ u ×   ∂ σ ∂ v

N = i → j → k → - a + r cos ⁡ v sin ⁡ u a + r cos ⁡ v cos ⁡ u 0 - r sin ⁡ v cos ⁡ u - r sin ⁡ v sin ⁡ u   r cos ⁡ v

N = a + r cos ⁡ v cos ⁡ u ⋅   r cos ⁡ v )   ,     ( a + r cos ⁡ v sin ⁡ u ⋅   r cos ⁡ v )   , (     a + r cos ⁡ v cos ⁡ u ⋅ r sin ⁡ v cos ⁡ u +   a + r cos ⁡ v sin ⁡ u ⋅ r sin ⁡ v sin ⁡ u

N = a + r cos ⁡ v r cos ⁡ u cos ⁡ v ,     sin ⁡ u cos ⁡ v , cos 2 ⁡ u + sin 2 ⁡ u   sin ⁡ v  

N = a + r cos ⁡ v r cos ⁡ u cos ⁡ v ,   sin ⁡ u cos ⁡ v ,   sin ⁡ v  

Passo 4

Uma superfície regular é toda arredondada, ou seja, não tem “bicos”. Como nosso tiroide é completamente arredondado, então é Regular.

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

A

σ u , v = a + r cos ⁡ v cos ⁡ u , a + r cos ⁡ v sin ⁡ u ,   r sin ⁡ v  

B

N = a + r cos ⁡ v r cos ⁡ u cos ⁡ v ,   sin ⁡ u cos ⁡ v ,   sin ⁡ v  

C

Nosso tiroide é completamente arredondado, então é Regular.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dada a esfera de raio 2 centrada na origem, encontre a equação do planto tangente a ela no ponto 1,1 , 2 , considerando a esfera como:b) Uma esfera de nível de F x , y , z = x 2 + y 2 + z 2 .
Considere a superfície parametrizada por φ r ,θ =r cos ⁡ θ ,r sin ⁡ θ ,θ ,0 ≤ r ≤ 1 , 0 ≤ θ ≤ 4 π b) Encontre uma expressão para um vetor normal à superfície
Considere a superfície parametrizada por φ r , θ = r cos ⁡ θ ,r sin ⁡ θ , θ ,0 ≤ r ≤ 1 ,0 ≤ θ ≤ 4 π c) Essa superfície é regular?
b) Encontre um vetor normal a esta superfície
c) Encontre a equação do plano tangente em (x_0 , y_0 , 0) .