Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 7.12 - Ex. 5

Considere a superfície S união de S 1 e S 2 , onde S 1 é dada por z = x 2 + y 2 , 0 ≤ z ≤ 2 2 , e S 2 é definida por x 2 + y 2 + z 2 = 16 , 8 ≤ x 2 + y 2 ≤ 16 e z ≥ 0 . Calcule o fluxo do campo vetorial

F x , y , z = y 2 x ,   z 2 y + x , x 2 z - 5

através da superfície S com campo de vetores normais exterior a S .

Passo 1

Se liga! O enunciado está pedindo para encontrar o fluxo. Para começarmos a resolver, podemos escrever que o fluxo, que chamaremos de ϕ , é dado por

ϕ = ∬ S F →     .     n →   d S .

Passo 2

O enunciado pede para achar o fluxo do campo através da união entre as superfícies S 1 e S 2 , ou seja, S 1 ∪ S 2 .

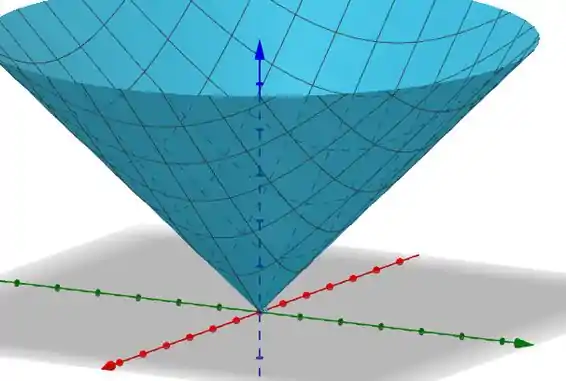
Outra informação importante é que a superfície S 1 é definida por

�� z = x 2 + y 2  

que representa um cilindro definido em 0 ≤ z ≤ 2 2 , podemos esboçar o desenho dele da seguinte forma.

Passo 3

A superfície S 2 é definida por

x 2 + y 2 + z 2 = 16

no intervalo 8 ≤ x 2 + y 2 ≤ 16 . Assim podemos esboçar o desenho

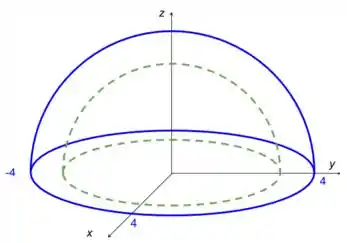
Onde o raio da semiesfera interna é 2 2 . A base superior do cone intercepta a semiesfera de raio 4 quando z = 2 2 .

Passo 4

A superfície S = S 1 ∪ S 2 não inclui a base da semiesfera ( x 2 + y 2 = 16 ). Chamaremos este disco de S A .

Repare que como queremos n A → exterior, teremos um fluxo saindo para baixo na direção z . Sendo assim

n A → = 0,0 , - 1 .  

Passo 5

Considerando que temos uma superfície fechada, podemos aplicar o Teorema de Gauss.

∬ S F →     .   n →   d s = ∭ W d i v F → d V     ( 2 )

Onde

d i v   F → = ∂ F 1 ∂ x + ∂ F 2 ∂ y + ∂ F 3 ∂ z .

Fazendo as derivadas parciais, temos

∂ F 1 ∂ x = ∂ ∂ x y 2 x = y 2

∂ F 2 ∂ y = ∂ ∂ y z 2 y + x = z 2

∂ F 3 ∂ z = ∂ ∂ z x 2 z - 5 = x 2

⇒ d i v   F → = x 2 + y 2 + z 2         ( 3 )

Passo 6

Podemos separar

∬ S ∪ S A F →     .   n →   d s

Em

∬ S A F →     .   n →   d s + ∬ S F →     .   n →   d s       ( 4 )

Substituindo a (4) em, (2) e usando a equação (3), temos

∭ W d i v F → d V = ∬ S A F →     .   n →   d s + ∬ S F →     .   n →   d s

Rearranjando, temos

∬ S F →     .   n →   d s = ∭ W d i v F → d V - ∬ S A F →     .   n →   d s   ( 5 )

Agora precisamos calcular as integrais do lado direito.

Passo 7

Vamos resolver a integral abaixo

∭ W d i v F → d V = ∭ W x 2 + y 2 + z 2   d z   d x   d y

Aqui precisamos prestar bastante atenção, pois na base inferior temos duas superfícies, a do cone ( C ) e a da semiesfera   ( E ) .

∭ W x 2 + y 2 + z 2   d z   d x   d y = P a r t e   C   + P a r t e     E     ( 6 )

Para o cone temos

0 ≤ z ≤ x 2 + y 2  

Como temos uma circunferência, mudaremos para coordenadas polares

x = r   c o s θ

y = r   s e n θ

d x   x y = r   d r d θ

Onde

0 ≤ r ≤ 2 2

0 ≤ θ ≤ 2 π

P a r t e   C = ∫ 0 2 π ∫ 0 2 2 ∫ 0 r ( r 3 + r z 2 ) d z d r d θ

= ∫ 0 2 π ∫ 0 2 2 r 4 + r 4 3   d r   d θ

Como θ não depende de r , podemos separar a integral

P a r t e   C = ∫ 0 2 π d θ ∫ 0 2 2 4 r 4 3   d r

= 2 π 2 2 5 3

Portanto

P a r t e   C = 1024 2 π 5

Passo 8

Para a semiesfera, temos

8 ≤ x 2 + y 2 ≤ 16  

Como temos uma circunferência, mudaremos para coordenadas polares

x = r   c o s θ

y = r   s e n θ

d x   x y = r   d r d θ

Onde

2 2 ≤ r ≤ 4

0 ≤ θ ≤ 2 π

P a r t e   E = ∫ 0 2 π ∫ 2 2 4 ∫ 0 16 - r 2 ( r 3 + r z 2 ) d z d r d θ

= ∫ 0 2 π ∫ 2 2 4 r 3 16 - r 2 + r 16 - r 2 3 2     d r   d θ

Como θ não depende de r , podemos separar a integral

P a r t e   E = ∫ 0 2 π d θ ∫ 2 2 4 r 3 16 - r 2 + r 16 - r 2 3 2   d r

= 2 π 128 2 3 + 128 2 5 = 2048 2 15

Retornando a equação (6), temos

∭ W d i v F → d V = 2048 2 15 - 1024 2 π 15 = 1024 2 π 5     ( 7 )

Passo 9

Agora resolver a integral abaixo

∬ S A F →     .   n →   d s

Como já vimos n A → = 0,0 , - 1 . Para z = 0 , temos

F x , y , 0 = y 2 x ,   x , - 5

Assim podemos substituir esses valores na integral

∬ S A y 2 x ,   x , - 5 0,0 , - 1   d x   d y = ∬ S A 5   d x   d y = 5 ∬ S A d x   d y

Como sabemos que estamos lidando como uma circunferência de raio 4 , podemos dizer que o valor da integral acima é igual a área da circunferência.

∬ S A F →     .   n →   d s = 5   π   4 2 = 80 π       ( 8 )

Passo 10

Agora só precisamos substituir (7) e (8) na equação (5). Sendo assim, o fluxo através da superfície S é

∬ S F →     .   n →   d s = 1024 2 π 5 - 80 π = ( 1024 2 - 400 ) π 5 .

Resposta

∬ S F →     .   n →   d s = ( 1024 2 - 400 ) π 5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule ∬ σ u → ⋅ n →d S sendo σ a fronteira de B com normal exterior n → sendo: c )B = x , y , z ∈ R 3 x 2 + y 2 + z 2 ≤ 1 } e u → = x i → + y j → + z 2 k → .
Seja σ o gráfico de f ( x , y ) = x 2 + y 2 ,x 2 + y 2 ≤ 1 e seja n → a normal a σ com componente z ≤ 0 . Seja F → x , y , z = x 2 y i → - x y 2 j → + k → , calcule ∬ σ F → ⋅ n →d S ,
Calcule ∬ σ u → ⋅ n →d S sendo σ a fronteira de B com normal exterior n → sendo: B = x , y , z ∈ R 3 0 ≤ x ≤ 1 ,0 ≤ y ≤ xe0 ≤ z ≤ 4 } e u → = x y i → + y z j → + z 2 k → .
Seja r → = x i → + y k → + z k → e seja B um compacto ao qual o teorema da divergência se aplica. Prove: v o lB = 1 3 ∬ σ r → ⋅ n →d S Onde σ é a fronteira de B com normal exterior n → .
Calcule ∬ σ u → ⋅ n →d S sendo σ a fronteira de B com normal exterior n → sendo: e )B é o paralelepípedo 0 ≤ x ≤ 1 ,0 ≤ y ≤ 1e0 ≤ z ≤ 1 e u → = x 3 i → + y 3 j → + z 3 k → .