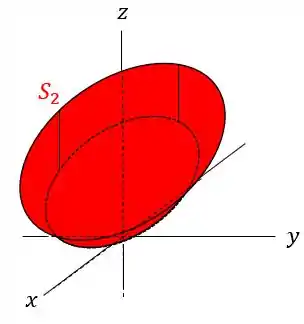
Considere a superfície S , união de S 1 e S 2 , onde S 1 tem equação x 2 + y 2 = 4 com 0 ≤ z ≤ 2 , e S 2 é o gráfico da função z = x 2 + y 2 definida no conjunto D , onde D = x ,y ∈ R 2|4 ≤ x 2 + y 2 ≤ 25 . a Esboce a superfície S 1 . b Esboce a superfície S 2 . c Esboce a superfície S .

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 3.2 - Ex. 2b

Considere a superfície , união de e , onde tem equação com , e é o gráfico da função definida no conjunto , onde .

Esboce a superfície .

Esboce a superfície .

Esboce a superfície .

Passo 1

Assim como a primeira parte do exercício, a superfície também possui uma superfície circular devido a sua equação ser dada por:

Ou ainda:

No entanto, há uma leve diferença. Pelo fato de ela possui um domínio tal que o valor de varia, isso significa que o valor de e, consequentemente, o valor do raio desse círculo também irão mudar.

Passo 2

Portanto, pegando o domínio, podemos concluir que a superfície será limitada por dois círculos de equações:

Ou seja, ela será limitada por um círculo superior de raio e outro inferior de raio .

Passo 3

Logo, se fizermos o esboço disso em uma visão tridimensional, teremos:

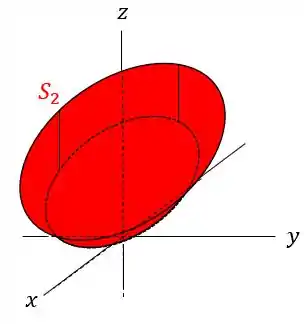
Para uma melhor noção da forma que ela possui, vamos esboçar a vista lateral dela no plano :

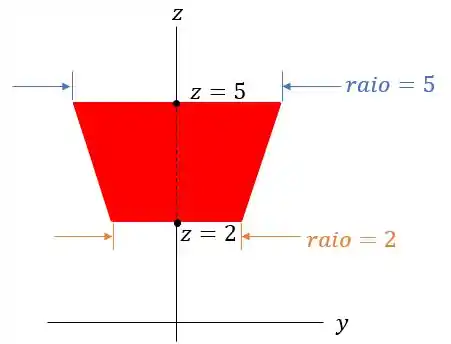
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dar a fronteira dos seguintes subconjuntos do R 2 . Representar graficamente. A = x , y ∈ R 2 x 2 + y 24

Identificar as afirmações verdadeiras:e) O conjunto B = { ( x ,y ) | x 2y 2 } é conexo.

Identificar quais dos conjuntos seguintes são bolas abertas em R 2 ou R 3 , determinando, em caso positivo, o centro e o raio. x 2 + y 2 + z2

Identificar as afirmações verdadeiras:d) O conjunto A = { ( x ,y ) | x 2 + 2 x + y 2 - 4 y0 } é conexo.

Identificar quais dos conjuntos seguintes são bolas abertas em R 2 ou R 3 , determinando, em caso positivo, o centro e o raio. x 2 + y 2 + 2 xx - 1 2 + y - 2 2