Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 3.7 - Ex. 4e
Identificar as afirmações verdadeiras:
e) O conjunto é conexo.
Passo 1
A definição prática de conjunto conexo é um conjunto que não tem nenhuma grande divisão que separe o conjunto todo em duas ou mais partes, de forma que elas não possam ser ligadas passando por fora do conjunto. Além disso, ele não pode ser um conjunto que se estende até o infinito
Passo 2
Então vamos ver se esse conjunto aí é conexo esboçando ele! Bom, se a gente desenhar, ele fica com essa cara aqui:
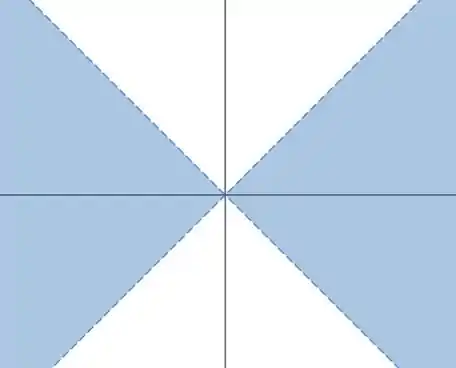
E como a gente pode ver, qualquer ponto da parte azul pode ser ligado com qualquer ponto da parte azul. Se a gente precisar passar do lado esquerdo pro lado direito, é só passar lá pela origem! Por isso, é conexo.
Resposta
Verdadeira.
Exercícios de Livros Relacionados
Identificar quais dos conjuntos seguintes são bolas abertas em R 2 ou R 3 , determinando, em caso positivo, o centro e o raio. x 2 + 4 x + y 25
Identificar as afirmações verdadeiras:d) O conjunto vazio é um conjunto aberto.
Identificar as afirmações verdadeiras:f) R 2 é um conjunto aberto.
Identificar as afirmações verdadeiras:g) Todo ponto de acumulação de um conjunto A pertence a esse conjunto.
Identificar as afirmações verdadeiras:b) Os pontos P ( 0 ,4 ) e Q ( 2 ,2 ) pertencem à fronteira do conjunto B = { x , y ∈ R 2 | y4 - x 2 } .