Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 3.16 - Ex. 2
Constatar, desenvolvendo exemplos graficamente, que as funções racionais do tipo , com e polinômios, tais que a diferença entre o grau do numerador e o grau do denominador é igual a , possui assíntotas inclinadas.
Passo 1
Vamos lá, galera, nessa aí a gente nem precisa fazer conta, só vamos jogar no programa de fazer gráfico e constatar essa parada. Montei algumas funções aqui, mas lembra que você pode montar a que quiser!
O gráfico dela fica assim:
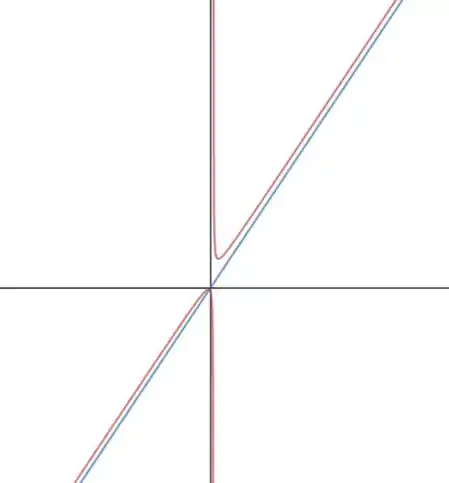
Esse gráfico tem assíntota na direção de .
Passo 2
Fazendo outra:
O gráfico dela fica assim:
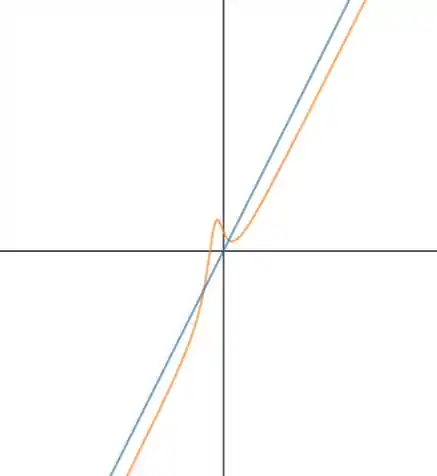
Ou seja, ela tem uma assíntota na direção de .
Passo 3
Fazendo mais umazinha:
Traçando o gráfico:
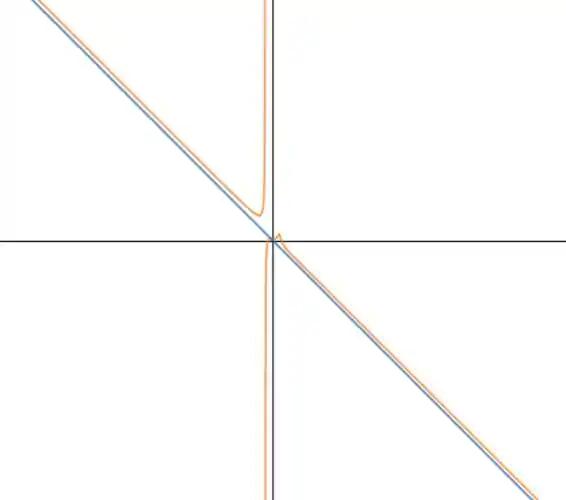
Ele tem uma assíntota na direção de .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Determine o limite de cada função a) quando QUOTE _x0001_
Determine o limite de cada função a) quando QUOTE _x0001_
Determine o limite da funçãoQUOTE _x0001_
Determine o limite de cada função b) quando QUOTE _x0001_
Determine o limite de cada função a) quando QUOTE _x0001_