Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.2 - Ex. 60
- Construa um polinômio que tenha raízes em .
- Esboce o gráfico de e de sua derivada juntos. Como o que você vê está relacionado com o teorema de Rolle?
- A função e sua derivada ilustram o mesmo fenômeno de e ?
Passo 1
Nos itens a e b da questão ele pede para que construamos um polinômio com as raízes apresentada e para isso utilizaremos a fatoração de polinômios com relação as suas raízes. Depois, pede para plotarmos os gráficos de juntos e relacionar ao teorema de Rolle. Por fim, deseja que mostremos se para a função temos o mesmo fenômeno apresentado em .
Passo 2
Seja um polinômio com n raízes e sejam elas podemos escrever esse polinômio em função de suas raízes como sendo
Para o nosso caso, as raízes serão , então, podemos escrever da seguinte forma
Lembrando que podemos reescrever assim
Aplicando a propriedade distributiva da multiplicação fazemos
Passo 3
Para resolvemos a letra b precisaremos saber quem é a derivada de para que possamos plotar no gráfico juntamente com a função que a gerou. Dessa forma, utilizando a regra de derivação de polinômio temos
Dessa forma, ficamos com
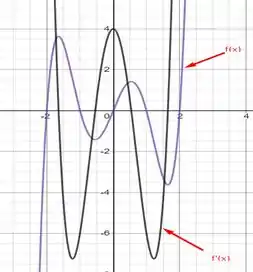
Percebemos pelo gráfico que cada ponto em quem intercepta está entre 2 pontos em que intercepta o eixo x como o esperado pelo teorema de Rolle.
Passo 4
Tomando agora a função sabemos que e que essas funções são defasadas de , sendo a função continua e diferenciável em a mesma propriedade de se aplica nesse caso.
Resposta
Ei, a resposta está no passo a passo :)