Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 2.17 - Ex. 1.a
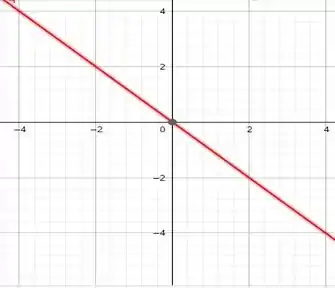
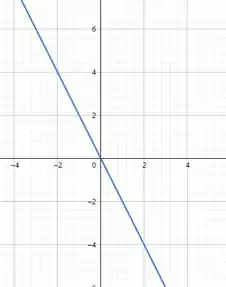
- Construir os gráficos da funções de grau. Dar o domínio e conjunto imagem.
-
; se
Passo 1
Inicialmente vamos determinar o domínio e a imagem, para qualquer função do grau, o domínio e a imagem são dados pelo conjunto dos números reais !
Passo 2
O que essas funções tem em comum?
Elas seriam o que chamamos de família de retas que tem coeficiente linear igual a , ou seja, todas as retas passam pelo ponto .
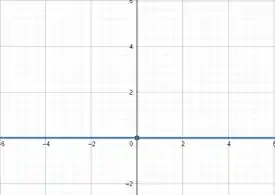
Para , temos:
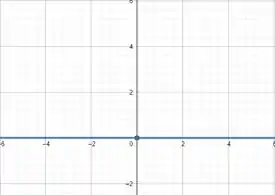
Para , temos , já temos um ponto, que é o , então só precisamos achar outro que pode ser o .
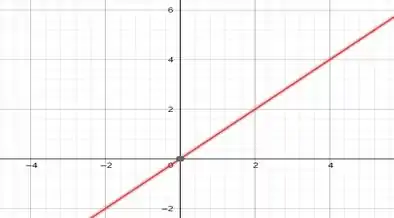
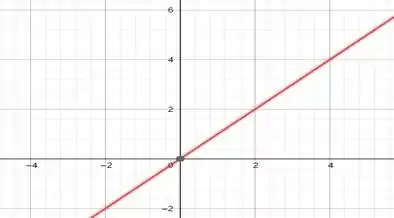
Para , temos , já temos um ponto, que é o , então só precisamos achar outro que pode ser o .
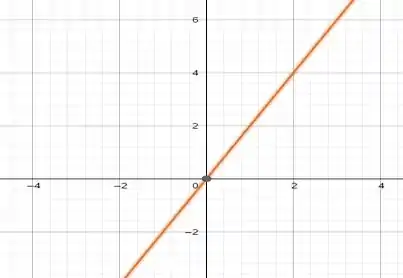
Passo 3
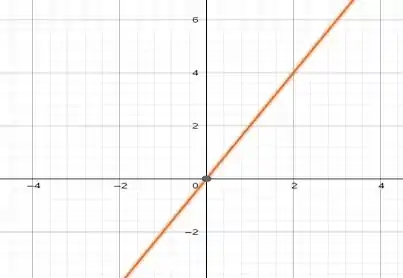
Para , temos , já temos um ponto, que é o , então só precisamos achar outro que pode ser o .
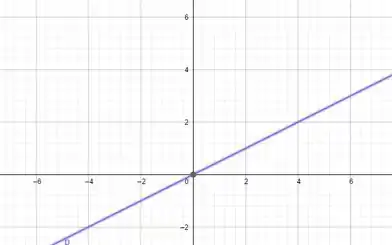
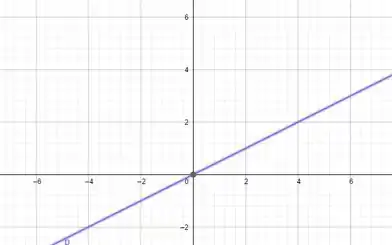
Para , temos , já temos um ponto, que é o , então só precisamos achar outro que pode ser o .
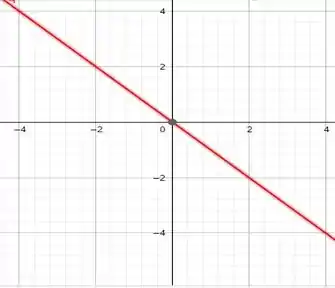
Para , temos , já temos um ponto, que é o , então só precisamos achar outro que pode ser o .
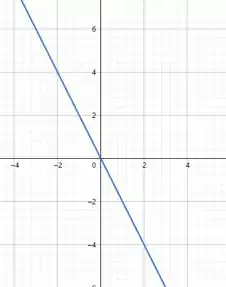
Resposta
