Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.5 - Ex. 7
Um estacionamento cobra $3 pela primeira hora ou fração, e $2 por hora sucessiva, ou fração, até uma máximo diário de $10.
a) Esboce o gráfico do custo do estacionamento como função do tempo decorrido.
b) Discuta as descontinuidades da função e seu significado para alguém que use o estacionamento.
Passo 1
Opa, bora lá! Nesse problema temos um estacionamento que cobra reais até a primeira hora e depois disso o preço é . O máximo total, como por exemplo o dia todo é .
Sabendo disso a gente primeiro precisa esboçar um gráfico onde o tempo vai no eixo e o preço no eixo !
Vamos pensar....
A questão explica uma situação problema e a utiliza como contextualização para um problema de continuidade de funções.
Na primeira hora (intervalo ) o preço será fixo e igual a $3. Na segunda hora (intervalo ), o preço será constante e igual a $5. Na terceira hora (intervalo ), o preço será constante e igual a $7. Na quarta hora (intervalo ), o preço será fixo e igual a $9. Por fim, como existe um limite diário de $10 para o preço, da quinta hora em diante () o preço será constante e igual a $10.
Passo 2
- O esboço pedido é dado por:
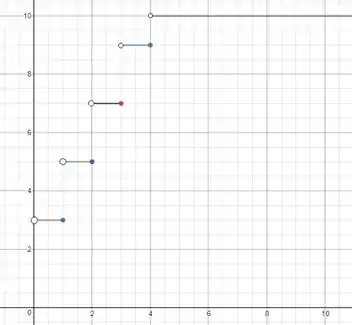
Passo 3
b) Vou utilizar a descontinuidade em para a discussão e estender para as demais descontinuidades pois o argumento é o mesmo.
Se uma pessoa deixar o carro exatamente uma hora no estacionamento ela pagará $3. Se ela deixar uma hora e 1 segundo ela já estará ocupando uma fração da segunda hora, de modo que deverá pagar $5. Assim, em existe um “salto” no preço que explica a descontinuidade no gráfico.
Sempre que houver uma passagem de hora o preço irá subir abruptamente causando a descontinuidade no gráfico.
Resposta
a) Esboço de gráfico.
b) Discussão.