Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 13.4 - Ex. 8
(Continuação do Exercício 7.)
- Utilize o método do Exercício 7 para encontrar N para a curva r(t) = ti + (1/3)t^3j quando t 0.
- Calcule N para t ≠ 0 diretamente de T utilizando a Equação 4 para a curva no item (a). N existe em t = 0? Desenhe a curva e explique o que está acontecendo a N conforme t passa de valores negativos para positivos.
Passo 1
Fala minha galera querida!! Vamos relembrar o método do n que aprendemos no exercício 7 e bora, recomendo rever o enunciado caso não se lembre.
- Primeiro vamos encontrar o parâmetro,
- Vamos calcular N agora no seguinte formato,
Utilizando para t > 0
Então, quando t
Passo 2
Já temos modulo de v do exercício anterior, então só achar T
Vamos achar o modulo
Temos tudo, só achar N agora.
Portanto, N não existe em t = 0, pois não se pode dividir nada por 0
Passo 2
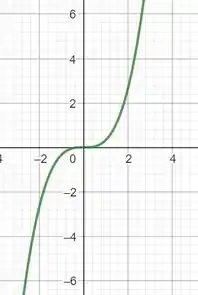
Bora desenhar a curva, no Geogebra, essa é a curva representada pela função vetorial, e .
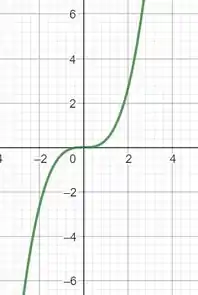Concluímos, então, que a curva possui concavidade para baixo, se x for menor do que 0, e concavidade para cima se x for maior do que 0.
Bora pro próximo.
Resposta
- Para t
N = 1 1 + t 4 t 2 i - j - , a curva muda sua concavidade quando t passa de negativo para positivo.
