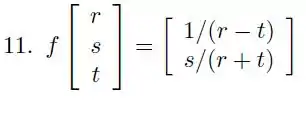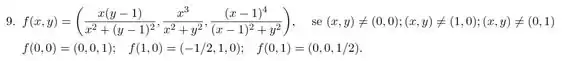Exercícios de Diferenciabilidade de Função Vetorial - Lista de Exercícios Resolvida

Mostre que a função

É diferenciável ou, se não for diferenciável, indique em que pontos não é diferenciável.

Mostre que a função

Se

É diferenciável ou, se não for diferenciável, indique em que pontos não é diferenciável.

Seja C a interseção das superfícies dadas por e . Qual dos seguintes pontos pertence à reta tangente a em ?

Escolha uma opção:

14. Se a função aplicada em um vetor não nulo é uma função real do seu comprimento , isto é, e se é diferenciável,

a) mostre que

b) determine quando

(Cap. 13.2 – Ex.49) Determine , onde , e .

Seja C a interseção das superfícies dadas por e . Qual dos seguintes pontos pertence à reta tangente a em ?

Escolha uma opção:

A superfície de nível da função que contém o ponto é o gráfico de uma função , diferenciável numa vizinhança de . O polinômio de Taylor de ordem 1 para , em torno do ponto é:

Escolha uma opção:

a)

b)

c)

d)

e)

A superfície de nível da função que contém o ponto é o gráfico de uma função , diferenciável numa vizinhança de . O polinômio de Taylor de ordem 1 para , em torno do ponto é:

Escolha uma opção:

a)

b)

c)

d)

e)

Determine o rotacional e o divergente dos campos vetoriais:

Determine o rotacional e o divergente dos campos vetoriais: