Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.4 - Ex. 41

Convertendo em integrais polares

  1. A maneira usual de calcular a integral imprópria ∫ 0 ∞ e - x 2 d x é primeiro calcular seu quadrado:

    2. I 2 = ∫ 0 ∞ e - x 2 d x ∫ 0 ∞ e - y 2 d y = ∫ 0 ∞ ∫ 0 ∞ e - x 2 + y 2 d x   d y

    Avalie a última integral utilizando coordenadas polares e resolva a equação resultante para I .

  2. Calcule:

lim x → ∞ ⁡ erf ⁡ x = lim x → ∞ ⁡ ∫ 0 x 2 e - t 2 π   d t

Passo 1

Faaaala, cara! Tranquileba?

Das coordenadas polares temos que:

x = r cos ⁡ θ

y = r   s e n θ

x 2 + y 2 = r 2

E em caso de dúvidas, vejamos a figura para que possamos entender melhor.

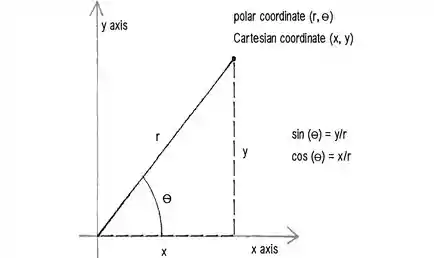
E em se tratando de integrais, quando transformamos uma integral para coordenadas polares, temos que adicionar o jacobiano das coordenadas polares, que no caso é r .

Passo 2

Sendo assim:

I 2 = ∫ 0 ∞ ∫ 0 ∞ e - x 2 + y 2 d y   d x

∫ 0 π 2 ∫ 0 ∞ e - r 2 r   d r   d θ

∫ 0 π 2 lim x → ∞ ⁡ ∫ 0 x r e - r 2 d r d θ

Fazendo u = - r 2 , logo d u = - 2 r d r , de forma que d r = - d u r d r .   Assim:

∫ 0 π 2 lim x → ∞ ⁡ ∫ 0 x - 1 2 e u   d u d θ

∫ 0 π 2 - 1 2 lim x → ∞ ⁡ ∫ 0 x e u d u d θ  

∫ 0 π 2 - 1 2 lim x → ∞ ⁡ e - x 2 - 1 d θ  

Se x → ∞ , e - x 2 → 0

∫ 0 π 2 1 2 d θ

1 2 θ 0 π 2

π 4

E logo:

I 2 = π 4 → I = π 2

Passo 3

Para b)

lim x → ∞ ⁡ erf ⁡ x = 2 π lim x → ∞ ⁡ ∫ 0 b e - t 2 d t  

2 π ∫ 0 ∞ e - t 2 d t

Que resulta em:

2 π e r f ⁡ ( x )

(caso não saiba, é chamada de (Função Erro))

Já a calculamos antes, isto é, é o I . Assim:

2 π π 2 = 1

Resposta

  1. I = π 2

2 π π 2 = 1

Exercícios de Livros Relacionados

Nos Exercícios 1-8, descreva a região dada em coordenadas polares.
Nos Exercícios 9-22, substitua a integral cartesiana por uma integral equivalente. Em seguida, calcule a integral polar. ∫ 0 2 ∫ 0 x yd yd x
Nos Exercícios 1-8, descreva a região dada em coordenadas polares. A região delimitada pela semicircunferência x 2 + y 2 = 2 y ,y ≥ 0
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.
Nos Exercícios 1-8, descreva a região dada em coordenadas polares.