Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 15.Exercícios Adicionais e Avançados - Ex. 12

a) Coordenadas polares Mostre, mudando para coordenadas polares, que

∫ 0 a sin ⁡ β ∫ y   c o t g   β a 2 - y 2 ln ⁡ x 2 + y 2 d x d y = a 2   β ( ln ⁡ a - 1 2   )  

Onde a > 0   e   0 < β < π 2  

b) Reescreva a integral cartesiana com a ordem de integracao invertida.

Passo 1

Faaaaalaaa meus abençoados, tudo blz?

Nesse primeiro passo na letra (a) ele nos da essa integral nada agradável (diga-se de passagem ) e pede para mudarmos para coordenadas polares, eu aqui montei um gráfico para vocês terem uma visão melhor da questão olha só

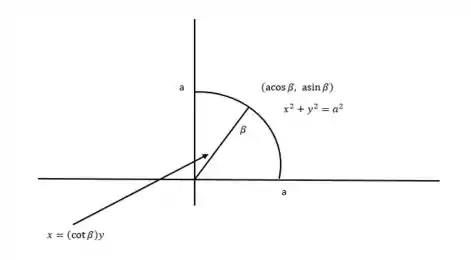
Agora realizando a mudança de coordenadas polares ficaremos,

∫ 0 a sin ⁡ β ∫ y   c o t g   β a 2 - y 2 ln ⁡ x 2 + y 2 d x d y =   ∫ 0 β ∫ 0 a r ln ⁡ r 2 d r d θ

u = r 2 d u = 2 r d r → 1 2   ∫ 0 β ∫ 0 a 2 ln ⁡ u   d u   d θ

Agora e so resolvermos a integral que vai ficar,

1 2   ∫ 0 β ∫ 0 a 2 ln ⁡ u   d u   d θ = 1 2   ∫ 0 β u ln ⁡ u - u 0 a 2 d θ

= 1 2   ∫ 0 β [ 2 a 2 ln ⁡ a - a 2 - lim t → 0 ⁡ t ln ⁡ t ]   d θ

= a 2 2   ∫ 0 β ( 2 ln ⁡ a - 1 ) d θ = a 2 β ( ln ⁡ a - 1 2 )    

Passo 2

Já na letra (b) ele pede para resolver a integral cartesiana com aordem de integração invertida

∫ 0 a cos ⁡ β ∫ 0 ( tan ⁡ β ) x ln ⁡ x 2 + y 2   d y d x + ∫ a cos ⁡ β a ∫ 0 a 2 - x 2 ln ⁡ x 2 + y 2   d y d x

Resposta

a)     a 2 β ( ln ⁡ a - 1 2 )    

b) ∫ 0 a cos ⁡ β ∫ 0 ( tan ⁡ β ) x ln ⁡ x 2 + y 2   d y d x + ∫ a cos ⁡ β a ∫ 0 a 2 - x 2 ln ⁡ x 2 + y 2   d y d x

Exercícios de Livros Relacionados

Calcule o valor da integral múltipla. ∫ ∫ D 1 1 + x 2d A ,o n d eDéar e g i ã ot r i a n g u l a rc o mv é r t i c e s0,0 ,1,1e0,1 é ã é
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.
Nos Exercícios 1-12, calcule a integral iterada.