Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.5 - Ex. 30
Uma cultura de bactérias começa com indíviduos e dobra de tamanho a cada meia hora.
a) Quantas bactérias existem após horas?
b) Quantas bactérias existem após horas?
c) Quantas bactérias existem após minutos?
d) Trace o gráfico da função população e estime o tempo para a população atingir bactérias.
Passo 1
Eaee, belezinha?? Bom... a questão nos diz que uma cultura de bactérias começa com indíviduos e dobra de tamanho a cada meia hora.
A partir disso, a questão quer que calculemos o tamanho da população de bactérias após e horas (esse último equivale a minutos).
Para isso, temos que relembrar um pouquinho das funções exponenciais.
Além disso, a questão também pede para traçarmos um gráfico da função população e estimar o tempo para a população atingir bactérias.
Para isso, a gente vai descobrir uma função exponencial e traçar esse gráfico.
E aí? Bora lá?? 😉
Passo 2
Bom... Esse é um problema típico sobre crescimento populacional exponencial.
A cada meia hora a população de bactérias dobra.
Assim, em horas, ela vai ter dobrado seis vezes:
Portanto, após horas, o tamanho da população será de bactérias.
Passo 3
Sabemos que a cada meia hora a população dobra de tamanho.
Assim, a população será dada por
onde é o número de períodos de meia hora. Assim, temos que
Portanto,
Passo 4
Para minutos, temos de hora.
Assim, basta fazer e aplicar na fórmula:
Passo 5
A seguir plotamos a função e a reta :
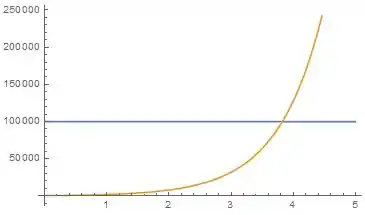
Vemos que a exponencial ultrapassa a reta aproximadamente em .
Assim, após aproximadamente horas a população de bactérias será superior a .