Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.2 - Ex. 36
- A curva é denominada serpentina. Encontre uma equação da reta tangente a essa curva no ponto
- Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a equação da reta tangente à curva , no ponto e fazer o gráfico delas. Pra isso, o primeiro passo é lembrar que a inclinação da reta tangente é obtida pela derivada da função:
E a equação da reta tangente é dada por:
Então precisamos achar a derivada da função e substituir na equação junto com o nosso ponto .
Em seguida, vamos plotar a nossa curva , junto com a reta tangente que encontrarmos, no gráfico.
Vamos lá!
Passo 2
Vamos começar encontrando a derivada da nossa função, que também será o coeficiente angular da nossa reta. Assim, derivando usando a regra do quociente, temos:
Simplificando:
Agora vamos verificar quanto a nossa derivada vale no ponto dado. Pra isso, basta substituir em e teremos:
Passo 3
Agora que já temos o coeficiente angular da nossa reta, basta substituir ele junto com ponto na equação da reta, que vimos no passo :
E teremos:
Isolando :
E acabamos? Não, ainda não! Falta o gráfico.
Passo 4
Traçando a nossa curva junto com a reta tangente , teremos o gráfico:
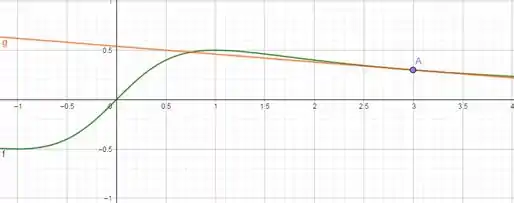
Repare que o ponto é o nosso ponto de tangência em .
Valeu, galera! Até a próxima! 😉