Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 3.3 - Ex. 30
Determine a derivada da função
Passo 1
Vamos la, essa é uma questão que já adianto, vai ficar grandinha! Mas já treinamos bastante antes. Estamos nerds bem espertos e sagazes agora. Vamos dar conta disso ; ) . O melhor, ainda podemos usar os truques de derivação que ajudam muito nossa vida. Vou passo – a – passo pra ninguém se perder no processo. Desta vez vamos usar a regra do quociente. Se lembra dela ? Pode deixar, vou botar aqui em baixo. Com o tempo essas regrinhas vão tão comuns na sua vida, que você irá lembrar já de automático.
Então temos que :
É quase igual à do produto, apenas alterando algumas coisinhas. Então, show! Vamos cair dentro do Cálculo. Aplicando a regra de derivação do quociente:
Passo 2
Cuidado aqui, tem muito termo você pode ficar confuso. Alguns termos vao sumir, então vai bem devagar.
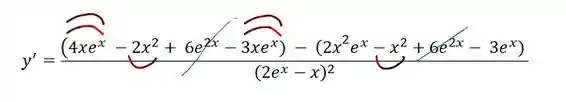
Chegamos a um ponto onde não podemos mais avançar com nossas contas, então acabamos por aqui. De início te aconselho a ir devagarzinho mesmo. Assim você vai pegar o ritmo e confiança. #Partiu #ProximaQuestão