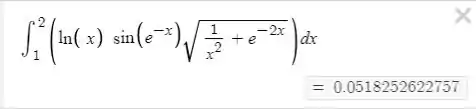29- Se é a curva com equações paramétricas , , , use uma calculadora ou CAS para calcular a integral de linha com precisão até a terceira casa decimal.
Passo 1
Utilizando a variável para fazer a integral de linha nós temos que fazer a seguinte integral parametrizada:
Passo 2
Isso nos daria a seguinte integral:
Utilizando o desmos encontramos um resultado dessa integral igual a: