Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.5 - Ex. 19
- Encontre a área da região sombreada na figura a seguir.
- Parece que, se o gráfico de , poderia ser assintótico às retas e . Sim ou não? Justifique sua resposta.
Passo 1
Fala gente tudo bem? Exercício um pouco complicadinho, mas nada impossível vem comigo.
Primeiro devemos conhecer quem é a nossa figura, para isso vamos utilizar o Geogebra para desenha-la.
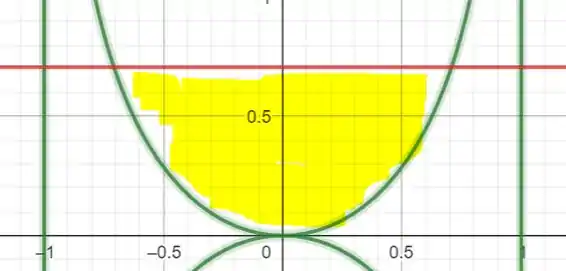Essa é a nossa figura:
Agora vamos calcular os pontos de intersecção das figuras, ou seja, os limites da integral:
Passo 2
Agora devemos entender quem são as áreas que devemos calcular.
Vamos traçar uma reta de modo a formar um triângulo na figura veja:
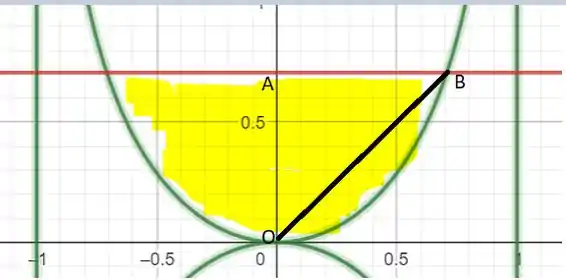
Temos o triangulo ABO, mas porquê? Para que fique mais fácil calcular a área da figura, pois basta saber a área do triângulo e soma-la a área da tampa que podemos descobrir através da nossa querida integral.
Passo 3
Para a área do triângulo vamos achar os comprimentos da base e da altura dele:
- AO, para acha-lo basta encontrar onde está o ponto A na reta , já que O representa a origem. A reta r cruza o eixo y quando .
- OB é a mesma estratégia, porém como mostrado na figura, ele intercepta em .
- Por fim, para encontrar AB, basta fazer Pitágoras:
A área do triangulo é
Passo 4
Para o cálculo da área só precisamos aplicar a fórmula da integral para áreas:
Passo 5
Agora só somar as áreas e multiplicar por 2 devido a simetria do eixo x:
Passo 6
- Precisamos descobrir qual é o limite a esquerda para a diferença entre a tangente e a assíntota , que nada mais é do que a função secante em coordenadas polares. Dessa forma descobriremos se ela é assíntota ou não.
Derivando para simplificar:
Dessa maneira, a tangente se aproxima da secante quanto mais chega perto de , e por isso, a secante de é uma assíntota vertical da tangente. Do mesmo modo a secante negativa também é uma assíntota vertical da tangente.
Resposta
- É assíntota, devido o ângulo se aproximar cada vez mais de em ambos os lados do eixo x.