Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 9.3 - Ex. 11

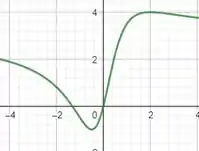
Seja f definida e derivável no intervalo ] - r , r [   r > 0 . Suponha que

f ' x = x 2 + f 2 x   p a r a   t o d o   x   e m   ] - r , r [ f 0 = 0                                                                                                                                        

  1. Mostre que 0 é ponto de inflexão horizontal.
  2. Mostre que f ' x > 0 para x ≠ 0 .
  3. Estude f com relação à concavidade
  4. Mostre que f x > 2 3 ! x 3 para 0 < x < r .
  5. Faça um esboço do gráfico de f .

Passo 1

Um ponto é ponto de inflexão horizontal quando sua f ' x = f ' ' x = 0 . Já que a primeira derivada já é dada, vamos encontrar a segunda derivada:

f ' ' x = f ' x '

f ' ' x = x 2 + f x 2 '

f ' ' x = 2 x + 2 f x f ' x

Agora vamos substituir x = 0 :

f ' ' 0 = 0 2 + f 2 0 = 0 + 0 2 = 0

f ' ' 0 = 2 ∙ 0 + 2 f 0 f ' 0 = 0 + 2 ∙ 0 ∙ 0 = 0

Portanto 0 é ponto de inflexão horizontal.

Passo 2

Vamos pensar na equação de f ' x :

f ' x = x 2 + f 2 x

Olhando para equação vemos que tem dois termos ao quadrado. Já que todo número do conjunto dos reais ao quadrado é positivo:

f ' x > 0 ,   s e   x ≠ 0

Passo 3

Como f ' x > 0 se x ≠ 0 a função é crescente. Logo se f ' ' x > 0 a concavidade é para cima e se f ' ' x < 0 a concavidade é para baixo. E se a função é crescente, no intervalo ] 0 , r [ a concavidade é para cima e no intervalo ] - r , 0 [ a concavidade é para baixo.

Passo 4

Vamos imaginar uma função h x onde h x é:

h x = f x - 2 3 ! x 3

Vamos derivar de cada lado essa equação:

h ' x = f ' x - 2 3 ! ∙ 3 x 2 = f ' x - x 2

h ' x = x 2 + f 2 x - x 2 = f 2 x

Como f x > 0 em ] 0 , r [ :

h ' x > 0 ,   s e   0 < x < r

Portanto, h é estritamente crescente nesse intervalo. Lembrando que h 0 = 0 :

h x > 0 ,   s e   0 < x < r

Logo,

h x > 0

f x - 2 3 ! x 3 > 0

f x > 2 3 ! x 3

Passo 5

Fazendo um esboço do gráfico de f :

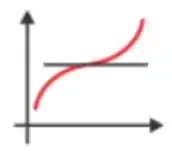
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

63-66. Suponha que a água esteja fluindo a uma taxa constante para dentro dos frascos mostrados. Faça um esboço grosseiro do gráfico do nível de água y versus tempo t . Assegure-se de que o esboço mos
63-66. Suponha que a água esteja fluindo a uma taxa constante para dentro dos frascos mostrados. Faça um esboço grosseiro do gráfico do nível de água y versus tempo t . Assegure-se de que o esboço mos
Encontre: (a) os intervalos onde f é crescente, (b) os intervalos onde f é decrescente, (c) os intervalos abertos onde f é côncava para cima, (d) os intervalos abertos onde f é côncava para baixo e (e
Encontre: (a) os intervalos onde f é crescente, (b) os intervalos onde f é decrescente, (c) os intervalos abertos onde f é côncava para cima, (d) os intervalos abertos onde f é côncava para baixo e (e
Encontre: (a) os intervalos onde f é crescente, (b) os intervalos onde f é decrescente, (c) os intervalos abertos onde f é côncava para cima, (d) os intervalos abertos onde f é côncava para baixo e (e