Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo Numérico - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.7 - Ex. 28

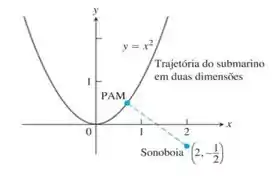
Nos problemas para localizar submarinos, normalmente é necessário determinar o ponto de aproximação máxima (PAM) em relação a uma sonoboia ( equipamento eletrônico flutuante que capta sinais sonoros de submarinos) na água. Suponha que o submarino se desloque em uma trajetória parabólica y   =   x 2 e que a sonoboia esteja localizada no ponto 2 ,   - 1 2 .

  1. Demonstre que o valor de x que minimiza a distância entre o submarino e a sonoboia é a solução da equação x   = 1 x 2 +   1 .
  2. Resolva a equação x   = 1 x 2 +   1 pelo método de Newton

Passo 1

Para a letra A desejamos mostrar que o valor que minimiza a distância entre o ponto dado e um ponto pertencente a função é dado por x   = 1 x 2 +   1 , devemos lembrar então que a distância entre dois pontos é dada por

d a , b = x - 2 2 + x 2 + 1 2 2 ,   x ≥ 0

Para um valor de x positivo a distância é mínima quando f x =   x - 2 2 + x 2 + 1 2 2 é mínimo, assim, precisamos na verdade minimizar a função f ( x ) . Feito isso, na letra b vamos precisar resolver a equação resultado pelo método de Newton que pode ser resumido pela seguinte fórmula

x n + 1 = x n - f ( x n ) f ' ( x n )

Passo 2

Para a letra a, vamos minimizar a função f ( x ) , primeiramente devemos achar os pontos críticos, ou seja, pontos onde teremos f ' x = 0 . Derivando nossa função obteremos

f ' x = 2 x - 2 + 2 x 2 + 1 2 ⋅ 2 x  

f ' x = 2 x - 2 + x 2 + 1 2 ⋅ 2 x

f ' x = 2 x - 2 + 2 x 3 + x

f ' x = 4 ⋅ ( x 3 + x - 1 )

Nesse caso, se derivamos a nossa função mais uma vez vamos obter

f " ( x )   =   4 ⋅ ( 3 x ²   + 1 )   >   0

Isso implica que os valores de x que encontrarmos fazendo f ' x = 0 serão pontos de mínimo, assim

f ' x = 4 ⋅ ( x 3 + x - 1 )

4 ⋅ x 3 + x - 1 = 0  

x 3 + x - 1 = 0

x 3 + x   = 1

x ⋅ x 2 + 1 = 1

x = 1 x 2 + 1

Passo 3

Para resolvermos a equação   x = 1 x 2 + 1 pelo método de Newton tomemos a função

g x = 1 x 2 + 1 - x

Sua derivada é dada por

g ' x =   - 2 x x 2 + 1 - 1

Aplicando no método de Newton utilizando x 0 = 1 vamos ter

x n + 1 = x n - 1 x n 2 + 1 - x n - 2 x n x n 2 + 1 - 1

x 0 + 1 = x 0 + 1 x 0 2 + 1 - x 0 2 x 0 x 0 2 + 1 + 1

x 1 = 1 + 1 1 + 1 - 1 2 ⋅ 1 1 2 + 1 + 1

x 1 = 1 + 1 2 - 1 2 2 + 1

x 1 = 1 + - 1 2 2

x 1 = 1 - 1 4 = 3 4 = 0.75

Repetindo esse procedimento vamos obter x 4 = 0.68233 com 5 casas decimais de precisão.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre uma raiz da equação: p ( x ) = x 4 - 6 x 3 + 10 x 2 - 6 x + 9 = 0 , aplicando o método de Newton para polinômios.
Use o método de Newton-Raphson para obter a menor raiz positiva das equações a seguir com precisão ϵ = 1 0 - 4 x 2 - t g ( x ) = 0 2 c o s ( x ) = e x 2 x 5 - 6 = 0
Seja f ( x ) = e x - 4 x 2 e ξ sua raiz no intervalo (0,1). Tomando x 0 = 0.5 , encontre ξ com ϵ = 1 0 - 4 , usando:o MPF com φ ( x ) = 1 2 e x / 2 ;o método de Newton.Compare a rapidez de convergênci
Método de Newton Modificado:Existe uma modificação no método de Newton na qual a função de iteração φ ( x ) é dada por φ ( x ) = x - f ( x ) f ' ( x 0 ) onde x 0 é a aproximação inicial e é tal que f
Seja f ( x ) = x 2 2 + x ( l n ( x ) - 1 ) . Obtenha seus pontos críticos com o auxílio de um método numérico.