Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 69
A curvatura no ponto da curva é definida como
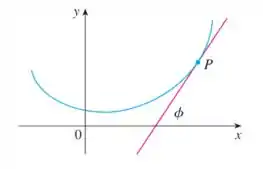
Onde é o ângulo de inclinação da reta tangente em como mostrado na figura. Então, a curvatura é o valor absoluto da taxa de variação de em relação ao comprimento de arco. Esta pode ser considerada uma medida da taxa da variação de direção da curva em e vai ser estudada em mais detalhes no Capítulo 13.
- Para a curva parametrizada deduza a fórmula
- Considerando uma curva como a curva parametrizada com o parâmetro , mostre que a fórmula na parte (a) se torna
Onde os pontos indicam as derivadas em relação a assim . [Sugestão: Use e a Equação 2 para encontrar . Então, use a Regra da Cadeira para achar ]
Passo 1
Eaee, belezinha??? Bom... o enunciado nos dá o seguinte gráfico:
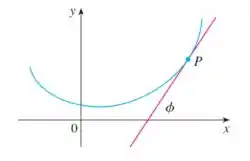
E diz que a curvatura no ponto é dada por:
Onde é o ângulo de inclinação da reta tangente em como mostrado na figura. Então, a curvatura é o valor absoluto da taxa de variação de em relação ao comprimento de arco.
Na letra (a) queremos deduzir a seguinte fórmula para uma curva parametrizada :
Onde os pontos indicam as derivadas em relação a assim .
Para isso, temos que usar e a Regra da Cadeira para achar .
Em seguida, na letra (b), devemos demonstrar a seguinte fórmula:
Agora bora lá!! 😉
Passo 2
(a) Sabemos que a curvatura no ponto é definida como
Vamos usar , derivando essa equação toda com relação a , ficamos com:
Mas sabemos da fórmula 2 que se , então
Assim, aplicando, temos:
Agora podemos substituir isso na nossa equação de :
Usando a regra da cadeia e o fato de que , temos que
Similarmente a fórmula 2, podemos dizer que , então
Então, se tivermos , ficamos com:
Passo 3
(b) Bom, temos que e
Então:
e
Agora podemos substituir isso na nossa fórmula do item (a):
Resposta
Demonstração