Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 41
41. Dada
Onde é um inteiro positivo. (a) Pare que valores de é derivável para todos os valores de x? (b) Para que valores de é contínua para todos os valores de x?
Passo 1
O que o enunciado está nos pedindo, em outras palavras, seria para mostrar, que para algum valor de n f será derivável para todo x e se encontrado os valores de n, ela será contínua para os mesmos valores de n. Assim, nesta questão devemos utilizar os conceitos necessários para que uma função seja derivável e contínua, conceito esses que foram vistos ao longo de praticamente todas questões dessa seção.
Passo 2
Letra (a)
Uma função f definida num intervalo aberto que contém x1 será derivável em x1 se e somente se 
ambas existirem e forem iguais.
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
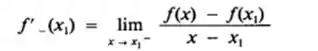
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
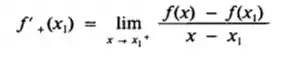
Passo 3
A derivada à esquerda de f(X) em x1 = 0 será:
Passo 4
A derivada à direita de f(X) em x1 = 0 será :
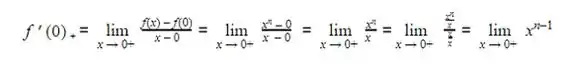
Passo 5
Como sabemos que para uma função ser derivável em um ponto sua derivada à direita deve ser igual à derivada à esquerda naquele ponto, Assim temos que
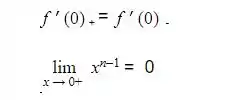
Isso só ocorre se n – 1 > 0 , ou seja , n > 1. Pois, para valores de n
Passo 6
Logo, os valores de n para os quais f é derivável para do x são tais que n percente ao intervalo aberto (1 , +∞).
Passo 7
Letra (b)
Como pode-se observar no teorema 3.2.1. se f for derivável em x1 , f será contínua em x1. Assim, como encontramos que f será derivável para todo n > 1, podemos afirmar que ela também f será contínua para todos os valores de x se e somente se n > 1.
Resposta
- n > 1
- n > 1