Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 6.1 - Ex. 64

R dada no Exercício 63 .Se o volume do solido formado pela revolução de R em torno do eixo x for 6 π e o volume do sólido formado pela revolução de R em torno da reta y = - 2 for 10 π , termine a área de R .

Passo 1

Inicialmente vamos analisar as informações que temos. Sendo assim, temos que volume do solido formado pela revolução de R em torno do eixo x for 6 π , ou seja,

V 1 = ∫ π f x 2 d x = 6 π

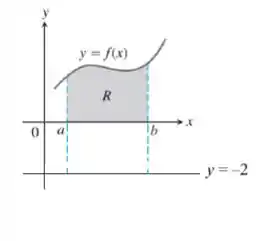
Por outro lado, sabemos que o volume do sólido formado pela revolução de R em torno da reta y = - 2 for 10 π . Isso significa que

V 2 = ∫ π f x + 2 2 d x = 10 π

Isso acontece devido a y = - 2 , temos que descer duas unidades no plano cartesiano,

Passo 2

Desejamos determinar a área de R . Para isso, façamos V 2 -   V 1 , sendo assim teremos,

V 2 -   V 1 = ∫ a b π f x + 2 2 d x - ∫ a b π f x 2 d x = 10 π - 6 π

⇒ ∫ a b f x + 2 2 - π f x 2 d x = 4 π

⇒ ∫ a b π ( f x 2 + 4 f ( x ) + 4 ) - π f x 2 d x = 4 π

⇒ π ∫ a b ( f x 2 +   4 f ( x ) + 4 ) - f x 2 d x = 4 π

⇒ π ∫ a b 4 f ( x ) + 4 d x = 4 π

⇒ 4 π ∫ a b f x + 1   d x = 4 π

⇒ ∫ a b f x + 1 d x = 1

⇒ ∫ a b f x d x + ∫ a b 1 d x = 1

⇒ ∫ a b f ( x ) d x + x ​ a b   = 1

⇒ ∫ a b f ( x ) d x = 1 - x ​ a b

⇒ ∫ a b f ( x ) d x = 1 - ( b - a )

⇒ ∫ a b f ( x ) d x = 1 - b + a

Como sabemos que a integral descrita dessa maneira representa a área então a área da região R é igual a 1 - b + a

Resposta

∫ a b f ( x ) d x = 1 - b + a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

8. Ache o volume do sólido gerado pela rotação da região limitada pela parábola y 2 = x , pelo eixo x e pela reta x = 4 em torno da reta x = 4 . Tome os elementos de área paralelos ao eixo de revoluçã
11. Determine o volume do sólido gerado pela rotação da região "triangular" limitada pelo eixo x, pela reta x = π / 3 e pela curva y = tan ⁡ x no primeiro quadrante em torno do eixo x.
14. Determine o volume do sólido gerado pela rotação em torno do eixo x da região limitada por y = 2 tg ⁡ x , y = 0 , x = - π / 4 e x = π / 4 . (A região está situada nos primeiro e terceiro quadrante
16. Volume de uma bola de futebol americano O perfil de uma bola de futebol americano se assemelha à elipse mostrada aqui. Determine o volume aproximado da bola de futebol até apolegada cúbica mais pr
12. Determine o volume do sólido gerado pela rotação da região limitada pela curva y = sin ⁡ x e pelas retas x = 0 , x = π e y = 2 em torno da reta y = 2 .