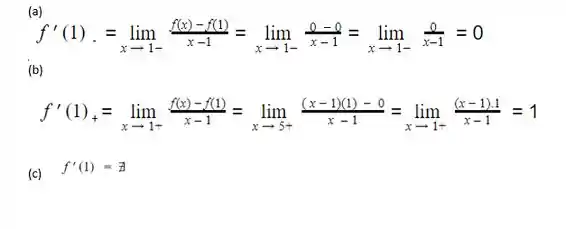Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 3.2 - Ex. 33
33. Dada . Faça um esboço do gráfico de para e [0,2]. Ache, se existirem: (a) (b) (c)
Passo 1
O esboço do gráfico da função pode ser obtido utilizando o programa de computador Symbolab Assim, o esboço do gráfico da função no intervalo fechado [ 0 , 2 ] é:
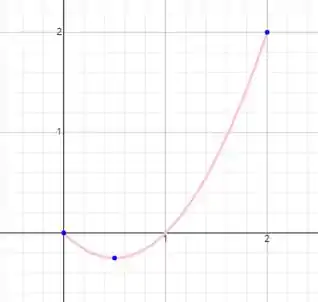
Passo 2
Nas letras (a) e (b) ele nos pede para determinar a derivada à esquerda e à direita de f (x) em x1 = 1. Porém, como ele nos dá um intervalo fechado para fazer a análise, devemos analisar como a função se comporta nesse intervalor dado. Ao substituir em [x] os números pertencentes ao intervalo [ 0, 2 ] concluímos que: f(x) = 0 , se 0 ≤ x
A derivada à esquerda de f em x1, denotada por f’ - (x1), será definda por
A derivada à direita de f em x1, denotada por f’ + (x1), será definda por
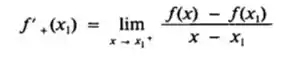
Passo 3
Letra (a)
A derivada à esquerda de f(X) em x1 = 1 será:
Passo 4
Letra (b)
A derivada à direita de f(X) em x1 = 1 será :
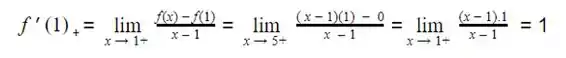
Passo 5
Letra (c)
Como, , podemos afirmar que 
.
Resposta
