Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 2.7 - Ex. 57
Dada a função definida por
Se for contínua em e for contínua em , podemos concluir que é contínua em ? Se sua resposta for sim, prove-a. Se sua resposta for não, que condição ou condições adicionais assegurariam a continuidade de em ?
Passo 1
O exercício fornece uma função dada que vale no intervalo e vale no intervalo , em que e são funções contínuas nos seus respectivos intervalos. A pergunta feita é se essas condições são suficientes para garantir que é contínua.
Para responder essa pergunta você deve lembrar qual o principal teste que você faz para testar que uma função definida por partes é contínua. Qual o ponto que você olha com carinho? O PONTO DE “COLAGEM”! Neste caso, o ponto de colagem é .
Além de e serem contínuas, elas têm que tender para o mesmo valor quando para que seja contínua.
Passo 2
Por exemplo, tomando , , , , , temos que
O gráfico de será
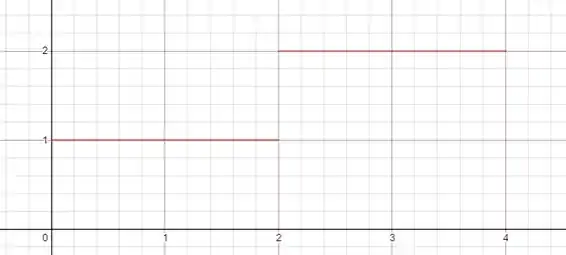
Mesmo com e contínuas, não é! Portanto, a resposta para a pergunta do problema é não!
Passo 3
A condição adicional que deve ser satisfeita para que seja contínua é que tanto quanto devem tender ao mesmo valor quando , isto é,
Resposta
Não.