Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.6 - Ex. 26
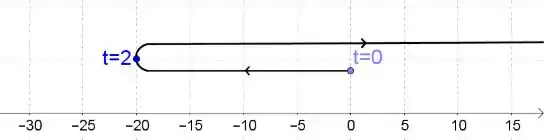
É dada uma função posição de uma partícula movendo-se ao longo de um eixo coordenado. Use o método do Exemplo para analisar o movimento da partícula em e faça um esboço esquemático do movimento (como o da Figura ).
Passo 1
Para analisar o movimento da partícula vamos achar a função velocidade derivando a função posição e a função aceleração, derivando a função velocidade, vamos lá:
Passo 2
Vamos agora analisar os sinais da função velocidade e da função aceleração:
Para a velocidade vamos ver :
É positiva em e negativa em .
Já é sempre positiva e assim aumenta constantemente.
A partícula acelera se a velocidade e a aceleração tiverem o mesmo sinal; e a partícula desacelera se a velocidade e a aceleração tiverem sinal oposto.
Assim a partícula desacelera em , para em e começa a acelerar em .
Passo 3
Vamos fazer um esboço esquemático do movimento:
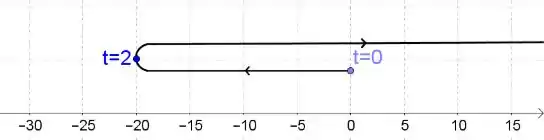
Resposta
