Dada a reta com equação e o ponto , (a) ache uma equação da reta passando por , perpendicular a e (b) a menor distância de à reta

Observe que a inclinação de é Queremos escrever uma reta que seja perpendicular a , para isso devemos achar a inclinação da nossa reta de forma que .

Assim,

Substituindo, na equação , o ponto dado e a inclinação encontrada anteriormente, temos

E essa é a nossa reta perpendicular.

Agora, temos que achar a menor distância do ponto à reta . Bem, a distância entre dois pontos a gente conhece, é assim:

Mas como assim a gente tem que achar a menor distância entre um ponto e uma reta???? Bem, uma reta é a união de infinitos pontos, então significa que tem infinitas (!) distâncias de um ponto até uma reta! É algo mais ou menos como essa figura aqui

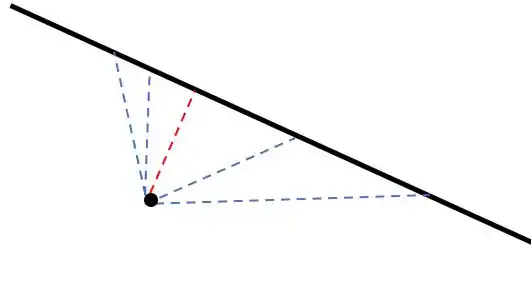
E aí tem uma dessas distâncias que é a menor de todas. Pela nossa figura, é a reta pontilhada em vermelho. Essa reta, tem uma coisa especial: ela é perpendicular à nossa primeira reta! E mais importante: nós já achamos a equação dessa reta no passo anterior!

Isso tudo significa que a menor distância entre o ponto e a reta preta é a distância entre o ponto e a interseção entre a reta preta e a reta vermelha pontilhada 😉

Vamos então achar essa interseção!

A interseção dessas duas retas se dá quando igualamos as equações das duas. A reta vermelha é dada por

E a reta preta é dada por

Igualando as duas ficamos com

Fazendo o MMC

Pra achar a coordenada desse ponto basta substituir esse valor de em qualquer uma das duas equações. Jogando na primeira...

Então a interseção entre as duas retas é o ponto

Agora vamos achar a distância entre esses dois pontos e

Jogando na calculadora

Beleza?