Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 3.4 - Ex. 63
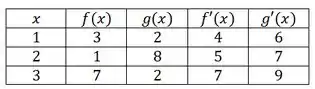
É dada uma tabela de valores para , , e .
a) Se , encontre .
b) Se , encontre .
Passo 1
Eaee, belezinha??
Bom... o enunciado nos dá a seguinte tabela que relaciona os valores de para as funções e suas derivadas:
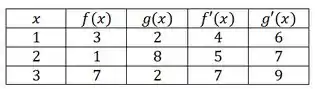
A partir dessa tabela, queremos encontrar a derivada dado que e também queremos encontrar a derivada dado que .
Parece complicado?
Podemos perceber que e são funções compostas e para calcular a derivada de um função composta o melhor método é a regra da cadeia;
Para resolver essa questão podemos apenas pegar a definição da regra da cadeia, onde temos que se:
Então:
Agora vamos aplicar!! 😉
Passo 2
Assim, no item a), como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
Se , temos
Na tabela podemos perceber que e , logo
Como de acordo com a tabela...
Tranquilo até aqui?
Passo 3
No item b), como queremos , ou seja, a derivada de no ponto , é só substituir esse valor na expressão:
Se , então
Na tabela vemos que e , logo
Tambem vemos que , portanto...
Entendeu direitinho?? Responde Aí 😉