Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 1.6 - Ex. 20
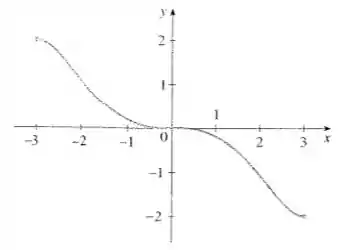
É dado o gráfico de .
- Por que é um a um?
- Determine o domínio e a imagem de
- Estime o valor de
Passo 1
Olá, meu querido amigo. Vamos resolver juntos mais uma atividade. Hoje iremos falar sobre funções um a um.
A função um a um (ou função bijetiva) é uma função em que cada elemento do domínio está relacionado a um único elemento do contradomínio e cada elemento do contradomínio está relacionado a um único elemento do domínio. Em outras palavras, não há repetição nos elementos associados.
Para identificar graficamente se uma função é uma função um a um, você pode usar o teste da linha horizontal:
1. Desenhe o gráfico da função.
2. Trace uma linha horizontal em todo o gráfico.
3. Veja se a linha horizontal cruza o gráfico em mais de um ponto em qualquer lugar.
Se a linha horizontal cruzar o gráfico em mais de um ponto em qualquer lugar, então a função não é uma função um a um.
Se a linha horizontal cruzar o gráfico em apenas um ponto em todos os lugares, então a função é uma função um a um.
Passo 2
Letra a)
Se criarmos linhas horizontais no gráfico dessa função, vamos notar que os gráficos só tocam a função em um ponto de cada vez. Sendo assim, temos aqui uma função um a um.
Letra b)
O domínio é o conjunto de todos os valores de que nossa função aceita. Já a imagem é o conjunto de todos os valores de que nossa função nos leva a partir entradas . Quando falamos de domínio e imagem de uma função inversa, deveremos trocar quem é o domínio e a imagem da função .
Para a função dada e no intervalo dado vamos ter que a função inversa vai ter como domínio e a imagem vai ser dada por
Passo 3
Letra c)
Por fim, para estimarmos o valor de tomemos o seguinte raciocínio
Se
então
Para o nosso caso, vamos ter
Resposta
Nossa função é um a um porque atende ao teste da linha horizontal, ou seja, nenhuma reta horizontal que você pegar vai tocar em dois pontos.
como domínio e a imagem vai ser dada por