Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.4 - Ex. 14
Dado que
ilustre a Definição 2 encontrando valores de que correspondam a , e .
Passo 1
Eaeee, belezinha?? Bom... o enunciado nos deu o seguinte limite:
Com isso, queremos ilustrar a Definição 2 dessa seção 2.4 encontrando valores de que correspondam a , e .
Mas que definição é essa??
Bom... a definição 2 diz o seguinte:
“Seja uma função definida em algum intervalo aberto que contenha o número , exceto possivelmente no próprio . Então dizemos que o limite de quando tende a é , e escrevemos:
Se para todo número houver um número tal que
Se então ”
Na nossa questão, vemos que , e .
Agora vamos aplicar!! 😉
Passo 2
Para , a definição de um limite requer que ache um tal que
O que implica em:
Se
Passo 3
Se plotarmos o gráfico de , e , vamos achar que:
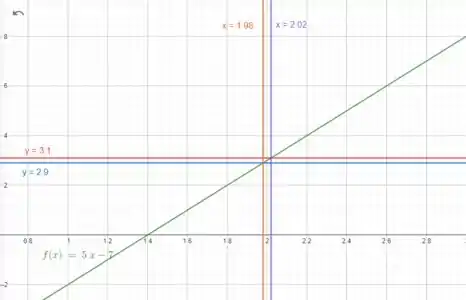
Passo 4
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é .
Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Passo 5
Para , a definição de um limite requer que ache um tal que:
O que implica em:
Se
Passo 6
Se plotarmos o gráfico de , e , vamos achar que:
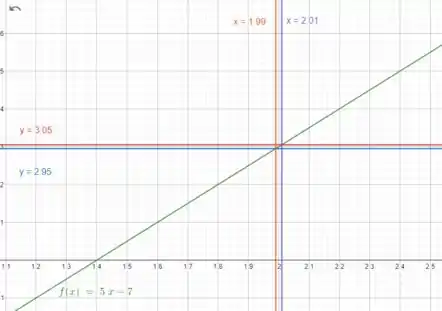
Passo 7
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é .
Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Passo 8
Para , a definição de um limite requer que ache um tal que
O que implica em:
se
Passo 9
Se plotarmos o gráfico de , e , vamos achar que:
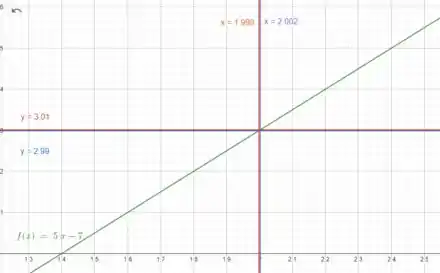
Passo 10
Vemos que a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é .
Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Resposta
Demonstração