Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 8.4 - Ex. 8
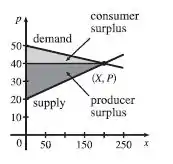
Para um dado produto, o número de unidades produzidas e o preço por unidade é determinado pelas coordenadas do ponto de intersecção das curvas de oferta e de demanda. Dadas as curvas de demanda e oferta , calcule os excedentes do consumidor e do produtor. Ilustre esboçando o gráfico das curvas de oferta e de demanda e identificando as áreas dos excedentes.
Passo 1
Bom galera, nessa questão queremos calcular o excedente do consumidor e do produtor. Para isso, utilizaremos a integral e depois iremos esboçar a curva de demanda e identificar o excedente como uma área.
Passo 2
Primeiramente, devemos encontrar os pontos de interseção das curvas do produtor e do consumidor. Igualando as equações temos
Resolvendo a equação, vemos que as curvas se interceptam em e em .
Para o consumidor, temos
Resolvendo a integral, temos
Passo 3
Aplicando os limites de integração, podemos encontrar o excedente do consumidor
Para o produtor, temos
Resolvendo a integral, temos
Aplicando os limites de integração encontramos o excedente do produtor
Esboçando graficamente ambas as curvas temos
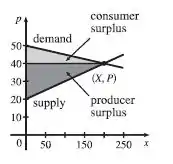
Resposta
