Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 65
É dado o seguinte gráfico de uma população de células de levedo em uma nova cultura de laboratório em função do tempo.
(a) Descreva como varia a taxa de crescimento populacional.
(b) Quanto a taxa é mais alta?
(c) Em quais intervalos a função população é côncava para cima ou para baixo?
(d) Estime as coordenadas do ponto de inflexão.
Passo 1
Fala aí, pessoal. Tudo certinho com vocês?
Bom, essa questão deu pra gente o seguinte gráfico
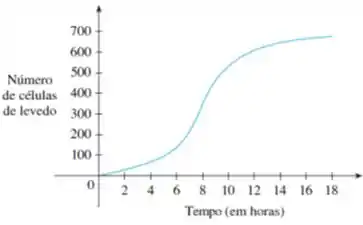
A questão diz que ele representa o crescimento populacional de células de levedo em uma nova cultura de laboratório em função do tempo.
Observando esse gráfico teremos que responder aos seguintes questionamentos:
(a) Descreva como varia a taxa de crescimento populacional.
Para isso temos que obser a velocidade com que a população está crescendo com o passar do tempo.
(b) Quanto a taxa é mais alta?
Para isso, basta olharmos onde essa velocidade é maior. Isso é indicado pela inclinação da reta tangente ao gráfico. Ou seja, onde essa reta é mais inclinada?
(c) Em quais intervalos a função população é côncava para cima ou para baixo?
Para isso, basta olharmos onde a velocidade de crescimento vai se acentuando, e onde vais ficando menos acentuada;
(d) Estime as coordenadas do ponto de inflexão.
O ponto de inflexão é onde ela muda esse comportamente.
Vem comigo que vamos encontrar cada uma dessas respostas no passo a passo.
Passo 2
Item a:
A função é crescente em todo o domínio, então a taxa de crescimento é sempre maior que zero. A função possui concavidade para cima até aproximadamente horas e concavidade para baixo a partir daí então a taxa de crescimento começa crescendo e passa a decrescer em cerca de horas.
Passo 3
Item b:
A taxa de crescimento populacional é a inclinação do gráfico.
A inclinação do gráfico é máxima em .
Isso significa que a taxa de crescimento populacional é máxima em
Passo 4
Item c:
A função possui concavidade para cima até aproximadamente horas e concavidade para baixo a partir daí então é côncava para cima no intervalo e côncava para baixo no intervalo .
Passo 5
Item d:
Se a função é côncava para cima no intervalo e côncava para baixo no intervalo então o momento em que o tempo é horas é o ponto de inflexão e a população nesse momento é de aproximadamente células de levedo. Logo, o ponto de inflexão é aproximadamente .
Resposta
(a) A função possui concavidade para cima até aproximadamente horas e concavidade para baixo a partir daí então a taxa de crescimento começa crescendo e passa a decrescer em cerca de horas
(b) Em aproximadamente em horas.
(c)A função é côncava para cima no intervalo e côncava para baixo no intervalo .
(d) O ponto de inflexão é aproximadamente .