Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.4 - Ex. 84

A figura mostra um setor de um círculo com ângulo central θ . Seja A θ a área do segmento entre a corda PR e o arco PR. Seja B ( θ ) a área do triângulo PQR. Encontre lim θ → 0 + ⁡ A ( θ ) / B ( θ ) .

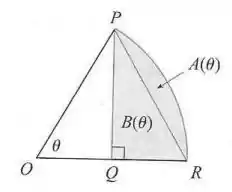
Passo 1

O exercício pede para calcularmos o limite da razão entre duas áres conforme o ângulo central θ tende a 0 .

A figura é a seguinte:

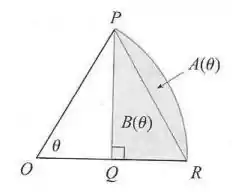
E queremos encontrar portanto, o seguinte limite:

lim θ → 0 + ⁡ A θ B θ

Para isso, devemos achar expressões para as áres A ( θ ) e B θ como função de θ e daí calcular o limite.

Passo 2

Vamos achar uma expressão para A ( θ ) :

Essa área será dada pela área do setor circular subtraindo-se a área do triângulo OPR:

A θ = A s e t o r - A Δ O P R

Vamos achar primeiro a área do setor circular. Consideremos que o raio do setor circular vale r .

π r 2 2 π = A s e t o r θ

*A equação acima é uma simples regra de três: a área do círculo todo está para 2 π radianos, enquanto que área do setor está para θ .

Assim,

A s e t o r = θ 2   r 2

Calculemos agora a área do triângulo POR. Da trigonometria no triângulo retângulo OQP:

s e n   θ = Q P O P

Sendo que o segmento O P é o próprio raio r do setor circular, portanto:

s e n   θ = Q P r  

Q P = r   s e n   θ

Assim, a área do triângulo OPR será:

A Δ O P R = b a s e ⋅ a l t u r a 2 = O R ⋅ Q P 2

E o segmento O R também é igual ao raio do setor circular, portanto:

A Δ O P R = r ⋅ r   s e n   θ 2 = r 2   s e n   θ 2

Desta forma,

A θ = A s e t o r - A Δ O P R = θ 2   r 2 - r 2   s e n   θ 2 = r 2 2   θ - s e n   θ

Passo 3

Agora vamos procurar uma expressão para B ( θ ) .

Aplicando trigonometria de triângulo retângulo no triângulo OQP:

cos ⁡ θ = O Q O P

Sendo que O P é o raio r do setor circular, portanto:

cos ⁡ θ = O Q r  

O Q = r cos ⁡ θ

Assim,

Q R = O R - O Q

E O R é o raio do setor circular, portanto:

Q R = r - r cos ⁡ θ = r   1 - cos ⁡ θ

Como já temos que Q P = r   s e n   θ , segue que B ( θ )

B θ = b a s e ⋅ a l t u r a 2 = Q R ⋅ Q P 2 = r 2   s e n   θ   ( 1 - cos ⁡ θ ) 2

Assim, a razão A ( θ ) / B ( θ ) será

A θ B θ = r 2 2   θ - s e n   θ r 2   s e n   θ   ( 1 - cos ⁡ θ ) 2 = θ - s e n   θ s e n   θ   ( 1 - cos ⁡ θ )

Passo 4

O limite que devemos calcular é

lim θ → 0 + ⁡ θ - s e n   θ s e n   θ   ( 1 - cos ⁡ θ )

Substituindo o valor do limite, temos:

0 - 0 0 1 - 1 = 0 / 0

Note que se trata de uma indeterminação do tipo 0/0, então podemos aplicar a regra de L’Hospital!!!

A derivada do numerador será

θ - s e n   θ ' = 1 - cos ⁡ θ

Já para o denominador, devemos aplicar uma regra do prodto:

s e n   θ   1 - cos ⁡ θ '

= cos ⁡ θ   1 - cos ⁡ θ + sen ⁡ θ 0 - - sen ⁡ θ

= c o s θ 1 - c o s θ + sen 2 ⁡ θ

Ajeitando isso aí:

= cos ⁡ θ - cos 2 ⁡ θ + sen 2 ⁡ θ

Assim, pela regra de L’Hospital:

lim θ → 0 + ⁡ θ - s e n   θ s e n   θ   1 - cos ⁡ θ = lim θ → 0 + ⁡ 1 - cos ⁡ θ cos ⁡ θ - cos 2 ⁡ θ + se n 2 ⁡ θ

Substituindo o limite, temos:

1 - 1 1 - 1 + 0 = 0 / 0

Seguimos com um indeterminação do tipo 0/0: vamos aplicar a regra de L’Hospital novamente:

lim θ → 0 + ⁡ 1 - cos ⁡ θ cos ⁡ θ - cos 2 ⁡ θ + se n 2 ⁡ θ = lim θ → 0 + ⁡ s e n   θ - sen ⁡ θ - 2 c o s θ - s e n θ + 2 s e n θ c o s θ

Ajeitando

lim θ → 0 + ⁡ s e n   θ - sen ⁡ θ + 4 c o s θ s e n θ

Aplicando o limite, temos:

0 - 0 + 4 ( 0 ) = 0 / 0

Novamente temos uma indeterminação do tipo 0/0: L’Hospital de novo:

lim θ → 0 + ⁡ s e n   θ - s e n   θ + 4 c o s θ s e n θ = lim θ → 0 + ⁡ cos ⁡ θ - cos ⁡ θ + 4 - s e n 2 θ + cos 2 ⁡ θ

Substituindo o limite, temos:

lim θ → 0 + ⁡ cos ⁡ θ - cos ⁡ θ + 4 - s e n 2 θ + cos 2 ⁡ θ = 1 - 1 + 4 - 0 + 1

= 1 - 1 + 4 = 1 3

Assim,

lim θ → 0 + ⁡ A ( θ ) B ( θ ) = 1 3

Resposta

1 / 3 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre o limite. Use a Regra de L’Hospital onde for apropriado. Se existir um método mais elementar, use-o. Se a regra de L’Hospital não for aplicável, explique por quê. lim x → 0 + ⁡ s e n x ln ⁡ x
Encontre o limite. Use a Regra de L’Hospital onde for apropriado. Se existir um método mais elementar, use-o. Se a regra de L’Hospital não for aplicável, explique por quê. lim x → - 2 ⁡x + 2 x 2 + 3 x
Calcule.underset(x - 1^-)(lim) (e^((1)/(x^2 - 1)))/(x - 1)
Para que valores de a e b temos underset(x - 0)(l i m) (t g 2 x)/(x^3) + (a)/(x^2) + (s i n ( b x ))/(x)
Encontre o limite. Use a regra de l’Hopital quando apropriado. Caso exista mais um método mais comum, use-o. Caso a regra de l’Hopital não se aplique, explique o porque. lim x → 0 + ⁡ 1 x - 1 tan - 1